��Ŀ����
����Ŀ���ó���һ���IJ���ֲ�����Ƴ����Ϊ���εĿ�ܣ���ͼ�٢��е�һ�֣���������AB=x�ף����������ͼ���ش��������⣺�����еIJ���ֲ����ܳ���ָ��ͼ�����к��ߵij��Ⱥͣ����кᵵ�������ֱ���AD��ABƽ�У�
��1����ͼ���У��������ֲ����ܳ���Ϊ12�ף���xΪ����ʱ�����ο��ABCD�����Ϊ3ƽ���ף�
��2����ͼ���У��������ֲ����ܳ���Ϊ12�ף���xΪ����ʱ�����ο��ABCD�����S����������Ƕ��٣�
���𰸡�
��1���⣺�����⣬BC�ij�Ϊ(4x)�ף������⣬�ã�
x(4x)=3����x4x+3=0����� x1=1��x2=3��
�𣺵�AB�ij���Ϊ1��3��ʱ�����ο��ABCD�����Ϊ3ƽ���ף�
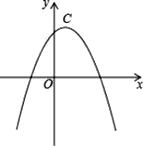
��2���⣺�������⣬��ͼ2�ã�AD=(124x)��3=4 ![]() x����S=ABAD=x(4
x����S=ABAD=x(4 ![]() x)=
x)= ![]() x+4x
x+4x
�䷽��S= ![]() ���൱x=
���൱x= ![]() ʱ��Sȡ���ֵ3��
ʱ��Sȡ���ֵ3��
�𣺵�x= ![]() ʱ�����ο��ABCD����������������3ƽ���ף�
ʱ�����ο��ABCD����������������3ƽ���ף�
����������1������ͼ�ο�֪AB+BC=4�����ú�x�Ĵ���ʽ��ʾ��BC�ij���Ȼ����ݾ��ε������ʽ�������̣���⼴�ɡ�
��2������ͼ�ڿ�֪4AB+3BC=12���ú�x�Ĵ���ʽ��ʾ��AD�ij����ٸ���S=ABAD������s��x�ĺ�����ϵʽ��Ȼ������������꣬������������

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�