Question

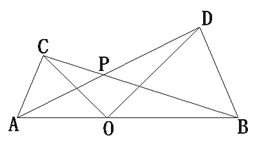
【题目】如图，点O为线段AB上任意一点（不与A、B重合），分别以AO、BO为一腰在AB的同侧作等腰△AOC和等腰△BOD，OA=OC，OB=OD，∠AOC与∠BOD都是锐角，且∠AOC=∠BOD ，AD与BC交于点P.

（1）试说明CB=AD；

（2）若∠COD =80°，求∠APB的度数．

Answer 1

【答案】（1）证明见解析；（2）∠APB=130°

【解析】

（1）证明∠AOD=∠COB，根据“SAS”证明全等；
（2）由∠COD=80°，∠AOC=∠BOD，求出∠AOC，根据△AOD≌△COB，得到∠OAD=∠OCB，由对顶角相等∠CMP=∠AMO，得到∠CPM=∠AOC=47°，根据邻补角求出∠APB．

（1）因为∠AOC=∠BOD

所以∠AOD=∠COB

在△AOD 与△COB中

因为OA=OC， ∠AOD=∠COB ，OD =OB

所以△AOD≌△COB

所以CB=AD

（2）因为∠COD=80°

所以∠AOC=∠BOD=50°

所以∠COB=130°

在△APB中

∠APB+∠1+∠2=180°

在△COB中

∠COB+∠3+∠2=180°

因为△AOD≌△COB

所以∠1=∠3

所以∠APB=∠COB

所以∠APB=130°