题目内容
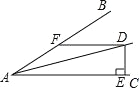
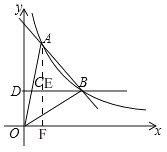
【题目】如图,一次函数y=kx+b与反比例函数y= ![]() 的图象在第一象限交于A、B两点,B点的坐标为(3,2),连接OA、OB,过B作BD⊥y轴,垂足为D,交OA于C,若OC=CA.
的图象在第一象限交于A、B两点,B点的坐标为(3,2),连接OA、OB,过B作BD⊥y轴,垂足为D,交OA于C,若OC=CA. 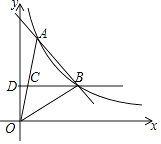
(1)求一次函数和反比例函数的表达式;
(2)求△AOB的面积.
【答案】
(1)解:如图,过点A作AF⊥x轴交BD于E,
∵点B(3,2)在反比例函数y= ![]() 的图象上,
的图象上,
∴a=3×2=6,
∴反比例函数的表达式为y= ![]() ,
,
∵B(3,2),
∴EF=2,
∵BD⊥y轴,OC=CA,
∴AE=EF= ![]() AF,
AF,
∴AF=4,
∴点A的纵坐标为4,
∵点A在反比例函数y= ![]() 图象上,
图象上,
∴A( ![]() ,4),
,4),
∴  ,
,
∴  ,
,
∴一次函数的表达式为y=﹣ ![]() x+6
x+6

(2)解:如图1,过点A作AF⊥x轴于F交OB于G,
∵B(3,2),
∴直线OB的解析式为y= ![]() x,
x,
∴G(2, ![]() ),
),
∵A(3,4),
∴AG=4﹣ ![]() =
= ![]() ,
,
∴S△AOB=S△AOG+S△ABG= ![]() ×
× ![]() ×3=4.
×3=4.
【解析】(1)先利用待定系数法求出反比例函数解析式,进而确定出点A的坐标,再用待定系数法求出一次函数解析式;(2)先求出OB的解析式式,进而求出AG,用三角形的面积公式即可得出结论.

练习册系列答案
相关题目