题目内容
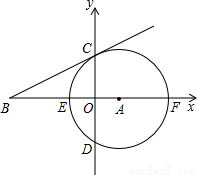
(2007•临夏州)在直角坐标系中,⊙A的半径为4,圆心A的坐标为(2,0),⊙A与x轴交于E、F两点,与y轴交于C、D两点,过点C作⊙A的切线BC,交x轴于点B.(1)求直线CB的解析式;
(2)若抛物线y=ax2+bx+c的顶点在直线BC上,与x轴的交点恰为点E、F,求该抛物线的解析式;
(3)试判断点C是否在抛物线上;
(4)在抛物线上是否存在三个点,由它构成的三角形与△AOC相似?直接写出两组这样的点.
【答案】分析:(1)连接AC,由Rt△AOC∽Rt△COB?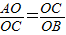 ,求得OB的长,即可得出确定B点坐标,进而可根据B、C坐标用待定系数法求得BC直线的解析式.
,求得OB的长,即可得出确定B点坐标,进而可根据B、C坐标用待定系数法求得BC直线的解析式.
(2)根据圆心的坐标及圆的半径不难得出E、F的坐标.根据抛物线和圆的对称性可知:抛物线顶点和圆心的横坐标必相等,据此可根据直线BC的解析式求出抛物线的顶点坐标.然后根据E、F及顶点坐标求出抛物线的解析式.
(3)在(1)中已经求得C点坐标,将C点坐标代入抛物线的解析式中进行判断即可.
(4)在(1)中已经求得∠OAC=60°,∠OCA=30°,如果连接CF,那么∠CFE= ∠OAC=30°,由于E、F同在抛物线上,因此连接CE后,三角形CEF就与三角形OAC相似.那么C、E、F就是符合条件的点.而根据抛物线的对称性可知,C点关于抛物线对称轴的对称点和E、F组成的直角三角形也应该符合条件.
∠OAC=30°,由于E、F同在抛物线上,因此连接CE后,三角形CEF就与三角形OAC相似.那么C、E、F就是符合条件的点.而根据抛物线的对称性可知,C点关于抛物线对称轴的对称点和E、F组成的直角三角形也应该符合条件.
解答: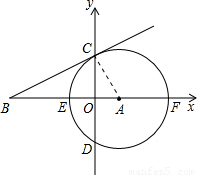 解:(1)方法一:
解:(1)方法一:
连接AC,则AC⊥BC.
∵OA=2,AC=4,
∴OC=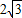 .
.
又∵Rt△AOC∽Rt△COB,
∴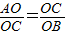 .
.
∴OB=6.
∴点C坐标为(0,2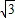 ),点B坐标为(-6,0).
),点B坐标为(-6,0).
设直线BC的解析式为y=kx+b,
可求得直线BC的解析式为y= x+2
x+2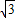 .
.
方法二:
连接AC,则AC⊥BC.
∵OA=2,AC=4,
∴∠ACO=30°,∠CAO=60°.
∴∠CBA=30°.
∴AB=2AC=8.
∴OB=AB-AO=6.
以下同证法一.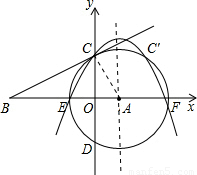
(2)由题意得,⊙A与x轴的交点分别为E(-2,0)、F(6,0),抛物线的对称轴过点A为直线x=2.
∵抛物线的顶点在直线BC上,
∴抛物线顶点坐标为(2,
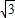 ).
).
设抛物线解析式为y=a(x-2)2+
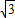 ,
,
∵抛物线过点E(-2,0),
∴0=a(-2-2)2+ ,
,
解得a=-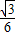 .
.
∴抛物线的解析式为y=- (x-2)2+
(x-2)2+
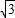 ,
,
即y=-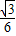 x2+
x2+ x+2
x+2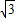 .
.
(3)点C在抛物线上.因为抛物线与y轴的交点坐标为(0,2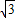 ),如图.
),如图.
(4)存在,这三点分别是E、C、F与E、C′、F,C′的坐标为(4,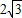 ).
).
即△ECF∽△AOC、△EC′F∽△AOC,如图.
点评:本题考查了圆的相关知识、二次函数解析式的确定、相似三角形的判定和性质等知识点.
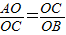 ,求得OB的长,即可得出确定B点坐标,进而可根据B、C坐标用待定系数法求得BC直线的解析式.
,求得OB的长,即可得出确定B点坐标,进而可根据B、C坐标用待定系数法求得BC直线的解析式.(2)根据圆心的坐标及圆的半径不难得出E、F的坐标.根据抛物线和圆的对称性可知:抛物线顶点和圆心的横坐标必相等,据此可根据直线BC的解析式求出抛物线的顶点坐标.然后根据E、F及顶点坐标求出抛物线的解析式.
(3)在(1)中已经求得C点坐标,将C点坐标代入抛物线的解析式中进行判断即可.
(4)在(1)中已经求得∠OAC=60°,∠OCA=30°,如果连接CF,那么∠CFE=
 ∠OAC=30°,由于E、F同在抛物线上,因此连接CE后,三角形CEF就与三角形OAC相似.那么C、E、F就是符合条件的点.而根据抛物线的对称性可知,C点关于抛物线对称轴的对称点和E、F组成的直角三角形也应该符合条件.
∠OAC=30°,由于E、F同在抛物线上,因此连接CE后,三角形CEF就与三角形OAC相似.那么C、E、F就是符合条件的点.而根据抛物线的对称性可知,C点关于抛物线对称轴的对称点和E、F组成的直角三角形也应该符合条件.解答:
 解:(1)方法一:
解:(1)方法一:连接AC,则AC⊥BC.
∵OA=2,AC=4,
∴OC=
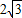 .
.又∵Rt△AOC∽Rt△COB,
∴
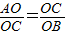 .
.∴OB=6.
∴点C坐标为(0,2
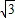 ),点B坐标为(-6,0).
),点B坐标为(-6,0).设直线BC的解析式为y=kx+b,
可求得直线BC的解析式为y=
 x+2
x+2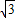 .
.方法二:
连接AC,则AC⊥BC.
∵OA=2,AC=4,
∴∠ACO=30°,∠CAO=60°.
∴∠CBA=30°.
∴AB=2AC=8.
∴OB=AB-AO=6.
以下同证法一.

(2)由题意得,⊙A与x轴的交点分别为E(-2,0)、F(6,0),抛物线的对称轴过点A为直线x=2.
∵抛物线的顶点在直线BC上,
∴抛物线顶点坐标为(2,

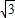 ).
).设抛物线解析式为y=a(x-2)2+

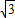 ,
,∵抛物线过点E(-2,0),
∴0=a(-2-2)2+
 ,
,解得a=-
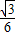 .
.∴抛物线的解析式为y=-
 (x-2)2+
(x-2)2+
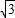 ,
,即y=-
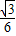 x2+
x2+ x+2
x+2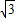 .
.(3)点C在抛物线上.因为抛物线与y轴的交点坐标为(0,2
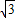 ),如图.
),如图.(4)存在,这三点分别是E、C、F与E、C′、F,C′的坐标为(4,
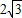 ).
).即△ECF∽△AOC、△EC′F∽△AOC,如图.
点评:本题考查了圆的相关知识、二次函数解析式的确定、相似三角形的判定和性质等知识点.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目