Question

（2007•临夏州）在平面几何中，我们可以证明：周长一定的多边形中，正多边形面积最大．使用上边的事实，解答下面的问题：
用长度分别为2、3、4、5、6（单位：cm）的五根木棒围成一个三角形（允许连接，但不允许折断），求能够围成的三角形的最大面积．

Answer 1

分析：根据已知得出取三边尽量接近，使围成的三角形尽量接近正三角形，则面积最大． 此时，三边为6、5+2、4+3，这是一个等腰三角形，再求出三角形的高，即可得出面积．

解答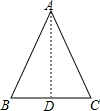：解：因为周长一定（2+3+4+5+6=20cm）的三角形中，以正三角形的面积最大．
取三边尽量接近，使围成的三角形尽量接近正三角形，则面积最大．    
此时，三边为6、5+2、4+3，这是一个等腰三角形．
即AB=AC=7cm，BC=6cm，
∴AD=

49-9

=2

10

（cm），
∴最大面积为：

1

2

×6×2

10

=6

10

（cm²）．

点评：此题主要考查了三角形面积求法以及正多边形的性质，根据已知得出三边为6、5+2、4+3时面积最大是解题关键．