题目内容
【题目】如图,在同一个平面内,![]() ,
,![]() .
.
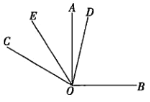
(1)填空:![]() ________;
________;
(2)如果OD平分![]() ,OE平分
,OE平分![]() ,那么
,那么![]() 的度数为;
的度数为;
(3)试问在(2)的条件下,如果将题目中![]() 改为
改为![]() ,其他条件不变,你能求出
,其他条件不变,你能求出![]() 的度数吗?若能,请你写出求解过程;若不能,请说明理由.
的度数吗?若能,请你写出求解过程;若不能,请说明理由.
【答案】(1)150°(2)45°(3)45°
【解析】
(1)直接根据已知利用∠BOC=∠AOB+∠AOC求出即可;
(2)利用角平分线的性质和(1)中所求得出答案即可;
(3)根据角平分线的性质∠DOC=![]() ∠BOC=45°+α,∠COE=
∠BOC=45°+α,∠COE=![]() ∠AOC=α,进而求出即可.
∠AOC=α,进而求出即可.
(1)∵∠AOB=90°,∠AOC=60°,
∴∠BOC=∠AOB+∠AOC=90°+60°=150°
故答案为:150°;
(2)∵OD平分∠BOC,OE平分∠AOC,
∴∠COD=![]() ∠BOC=75°,∠COE=
∠BOC=75°,∠COE=![]() ∠AOC=30°,
∠AOC=30°,
∴∠DOE的度数为:∠COD∠COE=45°;
故答案为:45°;
(3)∵∠AOB=90°,∠AOC=2α,
∴∠BOC=90°+2α,
∵OD、OE平分∠BOC,∠AOC,
∴∠DOC=![]() ∠BOC=45°+α,∠COE=
∠BOC=45°+α,∠COE=![]() ∠AOC=α,
∠AOC=α,
∴∠DOE=∠DOC∠COE=45°.

【题目】【问题情境】
已知矩形的面积为a(a为常数,a>0),当该矩形的长为多少时,它的周长最小?最小值是多少?
【数学模型】
设该矩形的长为x,周长为y,则y与x的函数表达式为y=2(x+![]() )(x>0).
)(x>0).
【探索研究】
小彬借鉴以前研究函数的经验,先探索函数y=x+![]() 的图象性质.
的图象性质.
(1)结合问题情境,函数y=x+![]() 的自变量x的取值范围是x>0,下表是y与x的几组对应值.
的自变量x的取值范围是x>0,下表是y与x的几组对应值.
x | … |
|
|
| 1 | 2 | 3 | m | … |
y | … | 4 | 3 | 2 | 2 | 2 | 3 | 4 | … |
①写出m的值;
②画出该函数图象,结合图象,得出当x= 时,y有最小值,y最小= ;
提示:在求二次函数y=ax2+bx+c(a≠0)的最大(小)值时,除了通过观察图象,还可以通过配方得到.试用配方法求函数y=x+![]() (x>0)的最小值,解决问题(2)
(x>0)的最小值,解决问题(2)
【解决问题】
(2)直接写出“问题情境”中问题的结论.