题目内容
已知:m,n,p均是实数,且mn+p2+4=0,m﹣n=4,则m+n= .
0
试题分析:由mn+p2+4=0可得出mn=﹣p2﹣4;将m﹣n=4的左右两边同时乘方,根据完全平方公式两公式之间的联系整理出(m+n)2,然后开方即可求出m+n的值.
解:∵mn+p2+4=0,m﹣n=4,
∴mn=﹣p2﹣4,(m﹣n)2=16,
∴(m+n)2﹣4mn=(m﹣n)2=16,
∴(m+n)2=16+4mn,
=16+4(﹣p2﹣4),
=﹣4p2;
∵m,n,p均是实数,
∴(m+n)2=﹣4p2≥0,
∴p=0,
∴m+n=0.
故答案是:0.
点评:本题考查了完全平方公式,关键是要灵活运用完全平方公式,整理出(m+n)2的形式.

练习册系列答案
 期末1卷素质教育评估卷系列答案
期末1卷素质教育评估卷系列答案
相关题目
 2y
2y ba3
ba3
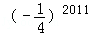 ×42012.
×42012.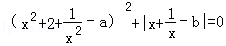 ,则a,b之间的关系式是 .
,则a,b之间的关系式是 .