题目内容
【题目】阅读下面材料:点A、B在数轴上分别表示实数a、b,A、B两点之间的距离表示为∣AB∣.
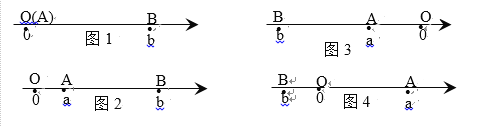
当A、B两点中有一点在原点时,不妨设点A在原点,
如图1,∣AB∣=∣OB∣=∣b∣=∣a-b∣;
当A、B两点都不在原点时,
如图2,点A、B都在原点的右边
∣AB∣=∣OB∣-∣OA∣=∣b∣-∣a∣=b-a=∣a-b∣;
如图3,点A、B都在原点的左边,
∣AB∣=∣OB∣-∣OA∣=∣b∣-∣a∣=-b-(-a)=∣a-b∣;
如图4,点A、B在原点的两边,
∣AB∣=∣OB∣+∣OA∣=∣a∣+∣b∣= a +(-b)=∣a-b∣;
回答下列问题:
(1)数轴上表示3和7的两点之间的距离是 ,数轴上表示-1和-3的两点之间的距离是 ,数轴上表示1和-2的两点之间的距离是 .
(2)数轴上表示x和-2的两点A和B之间的距离是 ,如果∣AB∣=2,那么x为 ;
(3)当代数式∣x∣+∣x-1∣取最小值时,最小值是 .
【答案】(1)4、2、3;(2)![]() 、0或-4(3)1
、0或-4(3)1
【解析】(1)4、2、3;
(2)数轴上表示x和-2的两点A和B之间的距离是![]() 如果∣AB∣=2,则x+2=2或-2
如果∣AB∣=2,则x+2=2或-2
得出x=0或-4
(3)当x在0和1之间时,∣x∣+∣x-1∣取最小值时1.

 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案【题目】某班要从甲、乙两名同学中选拔出一人,代表班级参加学校的一分钟踢毽子体能素质比赛,在一段时间内的相同条件下,甲、乙两人进行了六场一分钟踢毽子的选拔测试,根据他们的成绩绘制出如图的统计表和不完整的折线统计图.
甲、乙两人选拔测试成绩统计表
甲成绩 | 乙成绩 | |
第1场 | 87 | 87 |
第2场 | 94 | 98 |
第3场 | 91 | 87 |
第4场 | 85 | 89 |
第5场 | 91 | 100 |
第6场 | 92 | 85 |
中位数 | 91 | n |
平均数 | m | 91 |
并计算出乙同学六场选拔测试成绩的方差:
S乙2= ![]() =
= ![]()

(1)m= , n= , 并补全全图中甲、乙两人选拔测试成绩折线统计图;
(2)求甲同学六场选拔测试成绩的方差S甲2;
(3)分别从平均数、中位数和方差的角度分析比较甲、乙二人的成绩各有什么特点?
(4)经查阅该校以往本项比赛的资料可知,①成绩若达到90次/min,就有可能夺得冠军,你认为选谁参赛更有把握夺冠?为什么?
②该项成绩的最好记录是95次/min,就有可能夺得冠军,你认为选谁参赛更有把握夺冠?为什么?
【题目】如图,从左边第一个格子开始向右数,在每个小格子中都填入一个整数,使得其中任意三个相邻格子中所填整数之和都相等.
1 | ° | x | 7 | ﹣3 | … |
(1)可知x= ,= ,°= ;
(2)试判断第2016个格子中的数是多少?并给出相应的理由.
(3)判断:前n个格子中所填整数之和是否可能为2016?若能,求出n的值,若不能,请说明理由.