题目内容
已知:如图,BC是等腰△BED底边ED上的高,四边形ABEC是平行四边形。求证:四边形ABCD是矩形.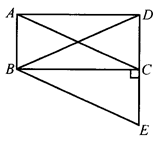

证明:∵BC是等腰△BED底边ED上的高,
∴EC=CD,………………1分
∵四边形ABEC是平行四边形,
∴AB∥CD,AB=CE=CD,AC=BE,………………2分
∴四边形ABCD是平行四边形.………………4分
∵AC=BE,BE=BD,………………5分
∴AC=BD,
∴四边形ABCD是矩形.………………6分
∴EC=CD,………………1分
∵四边形ABEC是平行四边形,
∴AB∥CD,AB=CE=CD,AC=BE,………………2分
∴四边形ABCD是平行四边形.………………4分
∵AC=BE,BE=BD,………………5分
∴AC=BD,
∴四边形ABCD是矩形.………………6分
根据平行四边形的性质可以证得AB与CD平行且相等,则四边形ABCD是平行四边形,再证得对角线相等即可证得

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
 ,高为12
,高为12

 的边长为
的边长为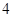 ,
,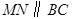 分别交
分别交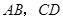 于点
于点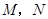 ,在
,在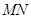 上任取两点
上任取两点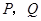 ,那么图中阴影部分的面积是 .
,那么图中阴影部分的面积是 .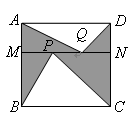
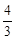 ,④
,④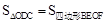 中,正确的有【 】
中,正确的有【 】