题目内容
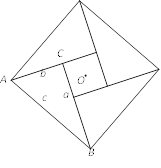
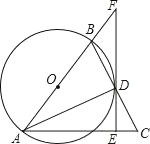
【题目】如图,△ABC中,AB=AC,以AB为直径的⊙O交BC边于点D,连接AD,过D作AC的垂线,交AC边于点E,交AB 边的延长线于点F.
(1)求证:EF是⊙O的切线;
(2)若∠F=30°,BF=3,求弧AD的长.
【答案】(1)见解析;(2)2π.
【解析】
(1)根据圆周角定理求出AD⊥BC,得出AD平分∠BAC,即可推出OD∥AC,推出OD⊥EF,根据切线的判定推出即可.
(2)由OD⊥DF得∠ODF=90°,利用含30度的直角三角形三边的关系OF=2OD,即OB+3=2OD,可解得OD=3,再计算出∠AOD=90°+∠F=120°,然后根据弧长公式求解.
证明:(1)连接AD,OD,

∵AB是直径,
∴∠ADB=90°,
即AD⊥BC,
∵AB=AC,
∴AD平分∠BAC,
∴∠OAD=∠CAD,
∵OA=OD,
∴∠OAD=∠ODA,
∴∠ODA=∠CAD,
∴OD∥AC,
∵DE⊥AC,
∴OD⊥EF,
∵OD过O,
∴EF是⊙O的切线.
(2)∵OD⊥DF,
∴∠ODF=90°,
∵∠F=30°,
∴OF=2OD,即OB+3=2OD,
而OB=OD,
∴OD=3,
∵∠AOD=90°+∠F=90°+30°=120°,
∴![]() 的长度=
的长度=![]() .
.

练习册系列答案
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
【题目】已知Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别是a,b,c,设△ABC的面积为S.
(1)填表:
三边a,b,c | S | c+b-a | c-b+a |
3,4,5 | 6 | ||
5,12,13 | 20 | ||
8,15,17 | 24 |
(2)①如果m=(c+b-a)(c-b+a),观察上表猜想S与m之间的数量关系,并用等式表示出来.
②证明①中的结论.