题目内容
【题目】如图:BD平分∠ABC,F在AB上,G在AC上,FC与BD相交于点H.∠GFH+∠BHC=180°,求证:∠1=∠2. 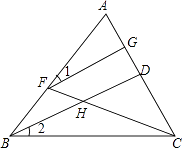
【答案】证明:∵∠BHC=∠FHD,∠GFH+∠BHC=180°, ∴∠GFH+∠FHD=180°,
∴FG∥BD,
∴∠1=∠ABD,
∵BD平分∠ABC,
∴∠2=∠ABD,
∴∠1=∠2.
【解析】求出∠GFH+∠FHD=180°,根据平行线的判定得出FG∥BD,根据平行线的性质得出∠1=∠ABD,求出∠2=∠ABD即可.
【考点精析】本题主要考查了平行线的判定与性质的相关知识点,需要掌握由角的相等或互补(数量关系)的条件,得到两条直线平行(位置关系)这是平行线的判定;由平行线(位置关系)得到有关角相等或互补(数量关系)的结论是平行线的性质才能正确解答此题.

练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
【题目】某校举行“汉字听写”比赛,每位学生听写汉字39个.比赛结束后随机抽查部分学生听写结果,图1,图2是根据抽查结果绘制的统计图的一部分.
组别 | 听写正确的个数x | 人数 |
A | 0≤x<8 | 10 |
B | 8≤x<16 | 15 |
C | 16≤x<24 | 25 |
D | 24≤x<32 | m |
E | 32≤x<40 | n |
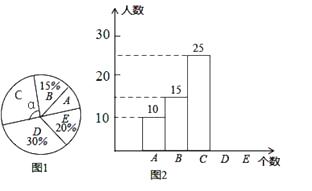
根据以上信息解决下列问题:
(1)本次共随机抽查了多少名学生,求出m,n的值并补全图2的条形统计图;
(2)求出图1中∠α的度数;
(3)该校共有3000名学生,如果听写正确的个数少于24个定为不合格,请你估计这所学校本次比赛听写不合格的学生人数