题目内容
【题目】如图,已知△ABC,∠C=90°,∠B=30°.
(1)用直尺和圆规在BC上找一点D,使DA=DB.(不写作法,保留作图痕迹)
(2)若BC=8,求点D到边AB的距离.
【答案】
(1)解:如图所示:点D即为所求;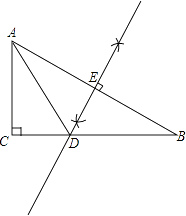
(2)解:∵DE是AB的垂直平分线,
∴AD=DB,DE⊥AB,
∴∠DAB=∠B=30°,
∵∠BAC=60°,
∴∠CAD=∠DAB=30°,
∵∠C=90°,DE⊥AB,
∴DC=DE,
∵DE⊥AB,∠B=30°,
∴BD=2DE,
∴BD=2DE,
∴DE= ![]()
【解析】(1)作AB的中垂线,交BC于点D,点D就是所求的点 ;
(2)根据中垂线的定义得出AD=DB,DE⊥AB,根据等边对等角得出∠DAB=∠B=30°,,根据角的和差得出∠CAD=∠DAB=30°,根据角平分线的性质得出DC=DE,根据含30°角的直角三角形的边之间的关系得出BD=2DE,根据线段的和差得出方程BD=2DE,解方程,得出DE的长 。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目