��Ŀ����
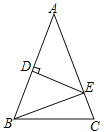
����Ŀ��(1)��ͼ(1),��֪���ڡ�ABC��,��BAC=90��,AB=AC,ֱ��m������A,BD��ֱ��m,CE��ֱ��m,����ֱ�Ϊ��D,֤��:��ABD�ա�ACE��DE=BD+CE��
(2)��ͼ(2),��(1)�е�������Ϊ���ڡ�ABC�У�AB=AC��D, A, E���㶼��ֱ��m�ϣ������С�BDA=��AEC=��BAC=a������aΪ������ǻ�۽ǣ����ʽ���DE=BD+CE�Ƿ����?��������������֤����������������˵������.

���𰸡�(1)��������(2)���������ɼ�������
��������
��1������BD��ֱ��m��CE��ֱ��m�á�BDA=��CEA=90��������BAC=90�������ݵȽǵ������ȵá�CAE=��ABD��Ȼ�������AAS�����ж���ADB�ա�CEA��
��AE=BD��AD=CE������DE=AE+AD=BD+CE��
��2�����á�BDA=��BAC=�������DBA+��BAD=��BAD+��CAE=180��-�����ó���CAE=��ABD�������ó���ADB�ա�CEA���ɵó��𰸣�
(1)��BD��ֱ��m��CE��ֱ��m��
���BDA=��CEA=90����
�ߡ�BAC=90��
���BAD+��CAE=90����
�ߡ�BAD+��ABD=90����
���CAE=��ABD��
���ڡ�ADB�͡�CEA��
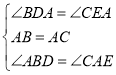
���ADB�ա�CEA(AAS)��
��AE=BD��AD=CE��
��DE=AE+AD=BD+CE��
(2)�ߡ�BDA=��BAC=����
���DBA+��BAD=��BAD+��CAE=180�����
���CAE=��ABD��
���ڡ�ADB�͡�CEA��
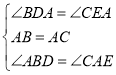 ��
��
���ADB�ա�CEA(AAS)��
��AE=BD��AD=CE��
��DE=AE+AD=BD+CE.

����Ŀ������ij��ѧ�������й���У�����������ִ������ߡ����в����ݳ����ɼ�����ѡ��5��ѡ����ɳ��д����Ӻ��д����Ӳμ�ѧУ�����������Ӹ�ѡ����5��ѡ�ֵľ����ɼ���ͼ��ʾ��

��1������ͼʾ��д�±���
ƽ�������֣� | ��λ�����֣� | �������֣� | |
���в� | 85 | ||
���в� | 85 | 100 |
��2��������ӳɼ���ƽ��������λ���������ĸ��ӵľ����ɼ��Ϻã�
��3���������Ӿ����ɼ��ķ���ж���һ��������ѡ�ֳɼ���Ϊ�ȶ���