题目内容
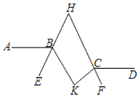
【题目】如图,点O为正方形ABCD对角线的交点,点E,F分别在DA和CD的延长线上,且AE=DF,连接BE,AF,延长FA交BE于G.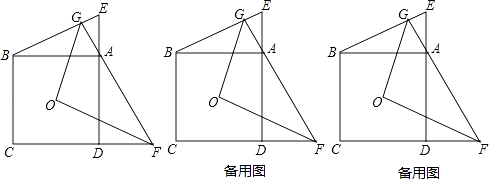
(1)试判断FG与BE的位置关系,并证明你的结论;
(2)连接OG,求∠OGF的度数;
(3)若AE= ![]() ,tan∠ABG=
,tan∠ABG= ![]() ,求OG的长.
,求OG的长.
【答案】
(1)解:FG⊥BE,
理由:∵四边形ABCD是正方形,
∴AB=AD,∠BAD=∠ADC=90°,
∴∠EAB=∠ADF=90°,
在△ABE与△DAF中, 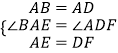 ,
,
∴△ABE≌△DAF,
∴∠E=∠AFD,
∵∠EAG=∠DAF,
∴∠AGE=∠ADF=90°,
∴FG⊥BE;
(2)解:连接OA,OB, 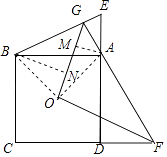
∵点O为正方形ABCD对角线的交点,
∴△AOB是等腰直角三角形,
∴∠AOB=90°,
∵∠AGB=90°,
∴A,G,B,O四点共圆,
∴∠AGO=∠ABO=45°;
(3)解:∵AE= ![]() ,tan∠ABG=
,tan∠ABG= ![]() ,
,
∴AB=2 ![]() ,
,
∴BE= ![]() =5,AO=BO=
=5,AO=BO= ![]() ,
,
∴AG= ![]() =2,
=2,
∴BG= ![]() =4,
=4,
过A作AM⊥OG于M,过B作BN⊥OG于N,
则△AGM,△BNG是等腰直角三角形,
∴BN=GN=2 ![]() ,AM=GM=
,AM=GM= ![]() ,
,
∵S四边形AGBO=S△AGB+S△AOB=S△BOG+S△AOG,
∴ ![]() AGBG+
AGBG+ ![]() AOBO=
AOBO= ![]() OGBN+
OGBN+ ![]() OGAM,
OGAM,
即 ![]() ×2×4+
×2×4+ ![]()
![]() =
= ![]() 2
2 ![]() OG+
OG+ ![]() OG,
OG,
∴OG=3 ![]() .
.
【解析】(1)根据正方形的性质得出AB=AD,∠BAD=∠ADC=90°然后证出△ABE≌△DAF,依据三角形全等的性质得出∠E=∠AFD,,从而得出结论;
(2)连接OA,OB,依据正方形的性质得出△AOB是等腰直角三角形,推出A,G,B,O四点共圆,根据圆周角定理得出结论;
(3)根据三角函数的定义得出AB的长,根据勾股定理得BE的长,OA=OB,根据三角形的面积公式得出AG的长,从而利用勾股定理得出BG的长,过A作AM⊥OG于M,过B作BN⊥OG于N,根据等腰直角三角形得性质得到BN=GN,AM=GM根据图形的面积列出方程即可求解。
【考点精析】解答此题的关键在于理解勾股定理的概念的相关知识,掌握直角三角形两直角边a、b的平方等于斜边c的平方,即;a2+b2=c2,以及对正方形的性质的理解,了解正方形四个角都是直角,四条边都相等;正方形的两条对角线相等,并且互相垂直平分,每条对角线平分一组对角;正方形的一条对角线把正方形分成两个全等的等腰直角三角形;正方形的对角线与边的夹角是45o;正方形的两条对角线把这个正方形分成四个全等的等腰直角三角形.

 53天天练系列答案
53天天练系列答案