题目内容
如图,已知AD⊥AB,DE平分∠ADC,CE平分∠BCD,且∠1+∠2=90°,那么BC⊥AB,说明理由。

如图:

∵DE,CE分别平分∠ADC,∠BCD
∴∠ADC=2∠1 ∠DCB=2∠2 (3分)
∵∠1+∠2=90°
∴∠ADC+∠BCD=180°
∴AD∥BC (6分)
∴∠A+∠B=180°
∵BC⊥AB∴∠A=90°
∴∠CBE=90°
∴CB⊥AB (8分)

∵DE,CE分别平分∠ADC,∠BCD
∴∠ADC=2∠1 ∠DCB=2∠2 (3分)
∵∠1+∠2=90°
∴∠ADC+∠BCD=180°
∴AD∥BC (6分)
∴∠A+∠B=180°
∵BC⊥AB∴∠A=90°
∴∠CBE=90°
∴CB⊥AB (8分)
利用两直线平行的性质和判定定理来求。

练习册系列答案
相关题目
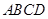 中,点
中,点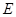 是线段
是线段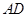 上的任意一点(
上的任意一点(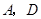 不重合),
不重合), 分别是
分别是 的中点.
的中点.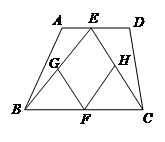
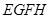 的形状并说明理由;
的形状并说明理由;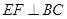 ,且
,且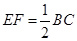 ,证明平行四边形
,证明平行四边形
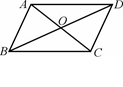

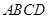 中,
中,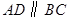 ,
,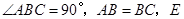 为
为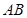 边上一点,
边上一点,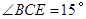 ,且
,且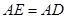 .连接
.连接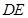 交对角线
交对角线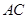 于
于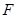 ,连接
,连接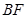 .下列结论:
.下列结论: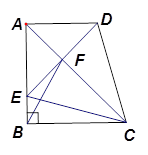
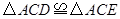 ;②
;②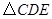 为等边三角形;
为等边三角形;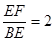 ;④
;④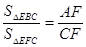 . 其中结论正确的是
. 其中结论正确的是 时,试说明点G为线段EF的中点;
时,试说明点G为线段EF的中点; ,FC=
,FC= ,用含有
,用含有 ,如图2,当
,如图2,当 时,讨论△
时,讨论△ 与△
与△ 是否相似,如果相似,请加以证明;如果不相似,只要写出结论,不要求写出理由.
是否相似,如果相似,请加以证明;如果不相似,只要写出结论,不要求写出理由.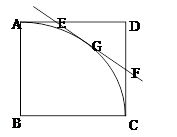

 ,AD=
,AD= .
.

