ЬтФПФкШн
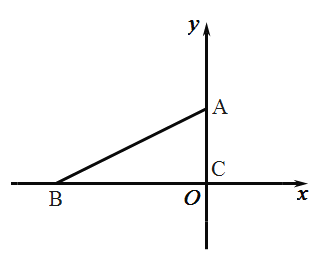
ЁОЬтФПЁПШчЭМЃЌжБЯпyЃНЉx+4гыxжсНЛгкЕуAЃЌгыyжсНЛгкЕуBЃЎХзЮяЯпyЃНЉ![]() x2+bx+cОЙ§AЃЌBСНЕуЃЌгыxжсЕФСэЭтвЛИіНЛЕуЮЊC
x2+bx+cОЙ§AЃЌBСНЕуЃЌгыxжсЕФСэЭтвЛИіНЛЕуЮЊC
ЃЈ1ЃЉЬюПеЃКbЃНЁЁ ЃЌcЃНЁЁ ЃЌЕуCЕФзјБъЮЊЁЁ ЃЎ
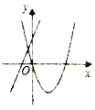
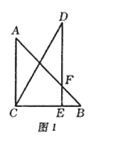
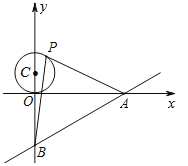
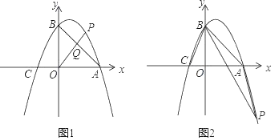
ЃЈ2ЃЉШчЭМ1ЃЌШєЕуPЪЧЕквЛЯѓЯоХзЮяЯпЩЯЕФЕуЃЌСЌНгOPНЛжБЯпABгкЕуQЃЌЩшЕуPЕФКсзјБъЮЊmЃЎPQгыOQЕФБШжЕЮЊyЃЌЧѓyгыmЕФЪ§бЇЙиЯЕЪНЃЌВЂЧѓГіPQгыOQЕФБШжЕЕФзюДѓжЕЃЎ
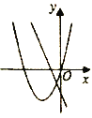
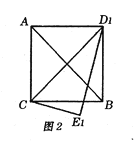
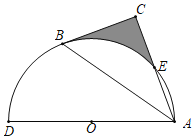
ЃЈ3ЃЉШчЭМ2ЃЌШєЕуPЪЧЕкЫФЯѓЯоЕФХзЮяЯпЩЯЕФвЛЕуЃЎСЌНгPBгыAPЃЌЕБЁЯPBA+ЁЯCBOЃН45ЁуЪБЃЎЧѓЁїPBAЕФУцЛ§ЃЎ
ЁОД№АИЁПЃЈ1ЃЉ1ЃЌ 4ЃЌCЃЈЉ2ЃЌ0ЃЉЃЛЃЈ2ЃЉyЃНЉ![]() m2+
m2+![]() m ЃЌPQгыOQЕФБШжЕЕФзюДѓжЕЮЊ
m ЃЌPQгыOQЕФБШжЕЕФзюДѓжЕЮЊ![]() ЃЛЃЈ3ЃЉSЁїPBAЃН12ЃЎ
ЃЛЃЈ3ЃЉSЁїPBAЃН12ЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉЭЈЙ§вЛДЮКЏЪ§НтЮіЪНШЗЖЈAЁЂBСНЕузјБъЃЌжБНгРћгУД§ЖЈЯЕЪ§ЗЈЧѓНтМДПЩЕУЕНbЃЌcЕФжЕЃЌСюy=0БуПЩЕУCЕузјБъЃЎ
ЃЈ2ЃЉЗжБ№Й§PЁЂQСНЕуЯђxжсзїДЙЯпЃЌЭЈЙ§PQгыOQЕФБШжЕЮЊyвдМАЦНааЯпЗжЯпЖЮГЩБШР§ЃЌевЕН![]() ЃЌЩшЕуPзјБъЮЊЃЈmЃЌ-
ЃЌЩшЕуPзјБъЮЊЃЈmЃЌ-![]() m2+m+4ЃЉЃЌQЕузјБъЃЈnЃЌ-n+4ЃЉЃЌБэЪОГіEDЁЂODЕШГЄЖШМДПЩЕУyгыmЁЂnжЎМфЕФЙиЯЕЃЌдйДЮРћгУ
m2+m+4ЃЉЃЌQЕузјБъЃЈnЃЌ-n+4ЃЉЃЌБэЪОГіEDЁЂODЕШГЄЖШМДПЩЕУyгыmЁЂnжЎМфЕФЙиЯЕЃЌдйДЮРћгУ![]() МДПЩЧѓНтЃЎ
МДПЩЧѓНтЃЎ
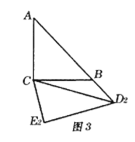
ЃЈ3ЃЉЧѓЕУPЕузјБъЃЌРћгУЭМаЮИюВЙЗЈЧѓНтМДПЩЃЎ
ЃЈ1ЃЉЁпжБЯпyЃНЉx+4гыxжсНЛгкЕуAЃЌгыyжсНЛгкЕуBЃЎ
ЁрAЃЈ4ЃЌ0ЃЉЃЌBЃЈ0ЃЌ4ЃЉЃЎ
гжЁпХзЮяЯпЙ§BЃЈ0ЃЌ4ЃЉ
ЁрcЃН4ЃЎ
АбAЃЈ4ЃЌ0ЃЉДњШыyЃНЉx2+bx+4ЕУЃЌ
0ЃНЉ![]() ЁС42+4b+4ЃЌНтЕУЃЌbЃН1ЃЎ
ЁС42+4b+4ЃЌНтЕУЃЌbЃН1ЃЎ
ЁрХзЮяЯпНтЮіЪНЮЊЃЌyЃНЉ![]() x2+x+4ЃЎ
x2+x+4ЃЎ
СюЉ![]() x2+x+4ЃН0ЃЌ
x2+x+4ЃН0ЃЌ
НтЕУЃЌxЃНЉ2ЛђxЃН4ЃЎ
ЁрCЃЈЉ2ЃЌ0ЃЉЃЎ
ЃЈ2ЃЉШчЭМ1ЃЌ

ЗжБ№Й§PЁЂQзїPEЁЂQDДЙжБгкxжсНЛxжсгкЕуEЁЂDЃЎ
ЩшPЃЈmЃЌЉ![]() m2+m+4ЃЉЃЌQЃЈnЃЌЉn+4ЃЉЃЌ
m2+m+4ЃЉЃЌQЃЈnЃЌЉn+4ЃЉЃЌ
дђPEЃНЉ![]() m2+m+4ЃЌQDЃНЉn+4ЃЎ
m2+m+4ЃЌQDЃНЉn+4ЃЎ
гжЁп![]() ЃНyЃЎ
ЃНyЃЎ
ЁрnЃН![]() ЃЎ
ЃЎ
гжЁп![]() ЃЌМД
ЃЌМД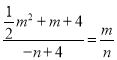
АбnЃН![]() ДњШыЩЯЪНЕУЃЌ
ДњШыЩЯЪНЕУЃЌ

ећРэЕУЃЌ4yЃНЉ![]() m2+2mЃЎ
m2+2mЃЎ
ЁрyЃНЉ![]() m2+
m2+![]() mЃЎ
mЃЎ
ymaxЃН ЃЎ
ЃЎ
МДPQгыOQЕФБШжЕЕФзюДѓжЕЮЊ![]() ЃЎ
ЃЎ
ЃЈ3ЃЉШчЭМ2ЃЌ

ЁпЁЯOBAЃНЁЯOBP+ЁЯPBAЃН45Ёу
ЁЯPBA+ЁЯCBOЃН45Ёу
ЁрЁЯOBPЃНЁЯCBO
ДЫЪБPBЙ§ЕуЃЈ2ЃЌ0ЃЉЃЎ
ЩшжБЯпPBНтЮіЪНЮЊЃЌyЃНkx+4ЃЎ
АбЕуЃЈ2ЃЌ0ЃЉДњШыЩЯЪНЕУЃЌ0ЃН2k+4ЃЎ
НтЕУЃЌkЃНЉ2
ЁржБЯпPBНтЮіЪНЮЊЃЌyЃНЉ2x+4ЃЎ
СюЉ2x+4ЃНЉ![]() x2+x+4
x2+x+4
ећРэЕУЃЌ![]() x2Љ3xЃН0ЃЎ
x2Љ3xЃН0ЃЎ
НтЕУЃЌxЃН0ЃЈЩсШЅЃЉЛђxЃН6ЃЎ
ЕБxЃН6ЪБЃЌЉ2x+4ЃНЉ2ЁС6+4ЃНЉ8
ЁрPЃЈ6ЃЌЉ8ЃЉЃЎ
Й§PзїPHЁЭcyжсгкЕуHЃЎ
дђSЫФБпаЮOHPAЃН![]() ЃЈOA+PHЃЉOHЃН
ЃЈOA+PHЃЉOHЃН![]() ЃЈ4+6ЃЉЁС8ЃН40ЃЎ
ЃЈ4+6ЃЉЁС8ЃН40ЃЎ
SЁїOABЃН![]() OAOBЃН
OAOBЃН![]() ЁС4ЁС4ЃН8ЃЎ
ЁС4ЁС4ЃН8ЃЎ
SЁїBHPЃН![]() PHBHЃН
PHBHЃН![]() ЁС6ЁС12ЃН36ЃЎ
ЁС6ЁС12ЃН36ЃЎ
ЁрSЁїPBAЃНSЫФБпаЮOHPA+SЁїOABЉSЁїBHPЃН40+8Љ36ЃН12ЃЎ