题目内容
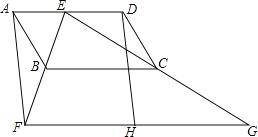
【题目】在平面直角坐标系中,如果点A,点C为某个菱形的一组对角的顶点,且点A,C在直线y=x上,那么称该菱形为点A,C的“极好菱形“.如图为点A,C的“极好菱形”的一个示意图.已知点M的坐标为(1,1),点P的坐标为(3,3).

(1)点E(2,4),F(3,2),G(4,0)中,能够成为点M,P的“极好菱形“的顶点的是 ;
(2)若点M,P的“极好菱形”为正方形,求这个正方形另外两个顶点的坐标;
(3)如果四边形MNPQ是点M,P的“极好菱形”.
①当点N的坐标为(3,1)时,求四边形MNPQ的面积;
②当四边形MNPQ的面积为12,且与直线y=x+b有公共点时,请写出b的取值范围.
【答案】(1)G;(2)正方形另外两个顶点的坐标为(1,3)、(3,1);(3)①S四边形MNPQ=4;②﹣6≤b≤6.
【解析】
(1)如图1中,观察图象可知:G能够成为点M,P的“极好菱形”顶点.
(2)先求得对角线PM的长,从而可得到正方形的边长,然后可得到这个正方形另外两个顶点的坐标.
(3)①先依据题意画出图形,然后可证明该四边形为正方形,从而可求得它的面积;
②根据菱形的性质得:PM⊥QN,且对角线互相平分,由菱形的面积为12,且菱形的面积等于两条对角线积的一半,可得QN的长,推出Q,N的坐标,再利用一次函数性质解决问题即可.
解:(1)如图1中,由题意点M,P的“极好菱形“的顶点,在线段PM的垂直平分线上.
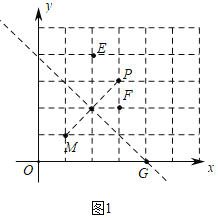
观察图象可知:满足条件的点是点G,
故答案为G.
(2)如图2所示:
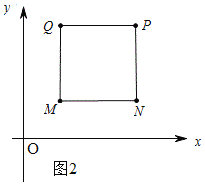
∵点M的坐标为(1,1),点P的坐标为(3,3),
∴MP=2![]() ,
,
∵“极好菱形”为正方形,其对角线长为2![]() ,
,
∴其边长为2.
∴这个正方形另外两个顶点的坐标为(1,3)、(3,1).
(3)①如图2所示:
∵M(1,1),P(3,3),N(3,1),
∴MN=2,PN⊥MN.
∵四边形MNPQ是菱形,
∴四边形MNPQ是正方形.
∴S四边形MNPQ=4..
②如图3所示:
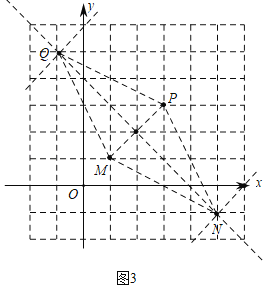
∵点M的坐标为(1,1),点P的坐标为(3,3),
∴PM=2![]() ,
,
∵菱形MNPQ的面积为12,
∴S菱形MNPQ=![]() PMQN=12,即
PMQN=12,即![]() ×2
×2![]() ×QN=12,
×QN=12,
∴QN=6![]() ,
,
∴Q(﹣1,5),N(5,﹣1),
当直线y=x+b经过点Q(﹣1,5)时,b=6,
当y=x+b经过点N(5,﹣1)时,b=﹣6,
∴当四边形MNPQ与直线y=x+b有公共点时,b的取值范围是﹣6≤b≤6.

 阅读快车系列答案
阅读快车系列答案