题目内容
如图,在梯形OABC中,CB∥OA,O为坐标原点,点C在y轴上,点A在x轴上,OC=4,tan∠OAB=2,以点B为顶点的抛物线经过O、A两点.求梯形OABC的面积.
【答案】分析:首先过点B作BD⊥x轴于点D.根据Rt△ABD中BD=OC=4,tan∠OAB=2,求得OA的长,再根据抛物线的性质求得BC、OA的长.最后运用梯形的面积计算公式求得最终值.
解答: 解:过点B作BD⊥x轴于点D,
解:过点B作BD⊥x轴于点D,
∵OC=4,
∴BD=OC=4,
∵tan∠OAB=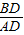 =2,
=2,
∴AD=2,
∵点D为OA的中点,
∴OA=4,BC=2,
∴S梯形OABC= =
=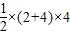 =12.
=12.
答:梯形OABC的面积为12.
点评:本题考查抛物线的性质:抛物线是轴对称图形.对称轴为直线x= ,对称轴与抛物线唯一的交点为抛物线的顶点P.
,对称轴与抛物线唯一的交点为抛物线的顶点P.
解答:
 解:过点B作BD⊥x轴于点D,
解:过点B作BD⊥x轴于点D,∵OC=4,
∴BD=OC=4,
∵tan∠OAB=
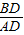 =2,
=2,∴AD=2,
∵点D为OA的中点,
∴OA=4,BC=2,
∴S梯形OABC=
 =
=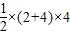 =12.
=12.答:梯形OABC的面积为12.
点评:本题考查抛物线的性质:抛物线是轴对称图形.对称轴为直线x=
 ,对称轴与抛物线唯一的交点为抛物线的顶点P.
,对称轴与抛物线唯一的交点为抛物线的顶点P. 
练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
 如图,在梯形OABC中,CB∥OA,O为坐标原点,点C在y轴上,点A在x轴上,OC=4,tan∠OAB=2,以点B为顶点的抛物线经过O、A两点.求梯形OABC的面积.
如图,在梯形OABC中,CB∥OA,O为坐标原点,点C在y轴上,点A在x轴上,OC=4,tan∠OAB=2,以点B为顶点的抛物线经过O、A两点.求梯形OABC的面积.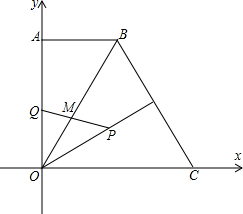 如图,直角梯形OABC中,AB∥OC,O为坐标原点,点A在y轴正半轴上,点C在x轴正半轴上,点B坐标为(2,
如图,直角梯形OABC中,AB∥OC,O为坐标原点,点A在y轴正半轴上,点C在x轴正半轴上,点B坐标为(2, 如图,在梯形OABC中,CB∥OA,O为坐标原点,点C在y轴上,点A在x轴上,OC=4,tan∠OAB=2,以点B为顶点的抛物线经过O、A两点.求梯形OABC的面积.
如图,在梯形OABC中,CB∥OA,O为坐标原点,点C在y轴上,点A在x轴上,OC=4,tan∠OAB=2,以点B为顶点的抛物线经过O、A两点.求梯形OABC的面积. (1)设从出发起运动了x秒,如果点Q的速度为每秒2个单位,试分别写出这时点Q在OC上或CB上时的坐标(用含x的代数式表示,不要求写出x的取值范围);
(1)设从出发起运动了x秒,如果点Q的速度为每秒2个单位,试分别写出这时点Q在OC上或CB上时的坐标(用含x的代数式表示,不要求写出x的取值范围);