题目内容
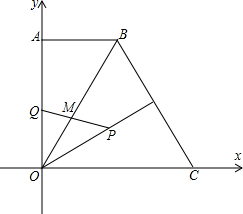 如图,直角梯形OABC中,AB∥OC,O为坐标原点,点A在y轴正半轴上,点C在x轴正半轴上,点B坐标为(2,2
如图,直角梯形OABC中,AB∥OC,O为坐标原点,点A在y轴正半轴上,点C在x轴正半轴上,点B坐标为(2,2| 3 |
(1)OH=
2
| 3 |
2
;| 3 |
(2)用含t(秒)的代数式表示点P和Q的坐标:P(
0
0
,t
t
),Q(3-
t
| ||
| 2 |
3-
t
,
| ||
| 2 |
| 3 |
| 1 |
| 2 |
| 3 |
| 1 |
| 2 |
(3)若△OPQ的面积为S(平方单位),求S与t之间的函数关系,并求t为何值时,△OPQ的面积最大,最大值是多少?
分析:(1)过点B作BG⊥OC于G,就可以得出OG=2,BG=2
,在Rt△BGC中由三角函数值就可以得出CG的值,从而得出OC,在Rt△OHC中由勾股定理就可以得出OH的值;
(2)过点P作PN⊥OC,就可以得出PN=
OP,ON=
PN,就可以表示出P、Q的坐标;
(3)由三角形的面积公式可以得出S△OPQ=
OQ•ON,将(2)求出的结论代入就可以求出结论.
| 3 |
(2)过点P作PN⊥OC,就可以得出PN=
| 1 |
| 2 |
| 3 |
(3)由三角形的面积公式可以得出S△OPQ=
| 1 |
| 2 |
解答:解:(1)过点B作BG⊥OC于G,
∵B坐标为(2,2
),
∴OG=2,BG=2
.
∵∠BCO=60°,
∴tan∠BCG=
=
,
∴
=
,
∴CG=2.
∴OC=4.
∵OH⊥BC,
∴∠OHC=90°,
∴∠COH=30°
∵cos30°=
=
,
∴
=
,
∴OH=2
.
(2)过点P作PN⊥OC,
∴∠PNO=90°,
∴PN=
OP,ON=
OP.
∵OQ=t,PH=t,
∴OP=2
-t,
∴PN=
-
t,ON=3-
t,
∴Q(0,t),P(3-
t,
-
t)
(3)∵S△OPQ=
OQ•ON,
∴S=
t•(3-
t),
S=-
t2+
t,
S=-
(t2-2
),
S=-
(t-
)2+
,
∵a=-
<0,
∴抛物线的开口向下,S有最大值,
∴t=
时,S最大=
.
∴S与t之间的函数关系为:S=-
t2+
t(0<t<2
),
t=
时,S最大=
.
故答案为:2
.
∵B坐标为(2,2
| 3 |
∴OG=2,BG=2
| 3 |
∵∠BCO=60°,
∴tan∠BCG=
| BG |
| CG |
| 3 |
∴
2
| ||
| CG |
| 3 |
∴CG=2.
∴OC=4.
∵OH⊥BC,
∴∠OHC=90°,
∴∠COH=30°
∵cos30°=
| OH |
| OC |
| ||
| 2 |
∴
| OH |
| 4 |
| ||
| 2 |
∴OH=2
| 3 |
(2)过点P作PN⊥OC,
∴∠PNO=90°,
∴PN=
| 1 |
| 2 |
| ||
| 2 |
∵OQ=t,PH=t,

∴OP=2
| 3 |
∴PN=
| 3 |
| 1 |
| 2 |
| ||
| 2 |
∴Q(0,t),P(3-
| ||
| 2 |
| 3 |
| 1 |
| 2 |
(3)∵S△OPQ=
| 1 |
| 2 |
∴S=
| 1 |
| 2 |
| ||
| 2 |
S=-
| ||
| 4 |
| 3 |
| 2 |
S=-
| ||
| 4 |
| 3 |
S=-
| ||
| 4 |
| 3 |
3
| ||
| 4 |
∵a=-
| ||
| 4 |
∴抛物线的开口向下,S有最大值,
∴t=
| 3 |
3
| ||
| 4 |
∴S与t之间的函数关系为:S=-
| ||
| 4 |
| 3 |
| 2 |
| 3 |
t=
| 3 |
3
| ||
| 4 |
故答案为:2
| 3 |
点评:本题考查了直角三角形的性质的运用,锐角三角函数值的运用,点的坐标的运用,三角形的面积公式的运用,二次函数的顶点式的运用,解答时运用直角三角形的性质根据三角函数值求解是关键,灵活运用抛物线的顶点式是难点.

练习册系列答案
 名师金手指领衔课时系列答案
名师金手指领衔课时系列答案
相关题目
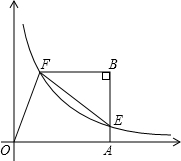 如图,直角梯形OABF中,∠OAB=∠B=90°,A点在x轴上,双曲线y=
如图,直角梯形OABF中,∠OAB=∠B=90°,A点在x轴上,双曲线y=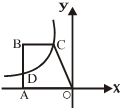 如图,直角梯形OABC中,∠OAB=∠B=90°,A点在x轴上,双曲线y=
如图,直角梯形OABC中,∠OAB=∠B=90°,A点在x轴上,双曲线y=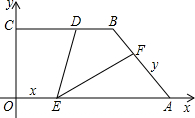 是BC上一点,BD=
是BC上一点,BD=