题目内容
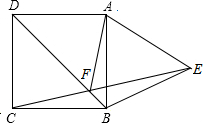 如图,以正方形ABCD的一边向形外作等边△ABE,BD与EC交于点F,且DF=EF,则∠AFD等于( )
如图,以正方形ABCD的一边向形外作等边△ABE,BD与EC交于点F,且DF=EF,则∠AFD等于( )| A、60° | B、50° | C、45° | D、40° |
分析:分别求证△DCF≌△DAF≌△EAF可得∠DFC=∠AFD=∠AFE,根据∠DFC+∠AFD+∠AFE=180°,可得∠DFC=∠AFD=∠AFE=60°
解答: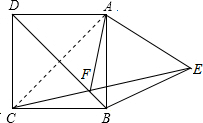 解:连接AC,
解:连接AC,
∵BD为AC的垂直平分线,
∴FA=FC,
∵四边形ABCD是正方形,
∴AD=DC=AB,
在△DCF和△DAF中,
,
∴△DCF≌△DAF,
∵三角形ABE是等边三角形,
∴AE=AB=AD,
在△DAF和△EAF中,
,
∴△DAF≌△EAF,
∴△DCF≌△DAF≌△EAF,
得:∠DFC=∠AFD=∠AFE,
又∵∠DFC+∠AFD+∠AFE=180°
∴∠DFC=∠AFD=∠AFE=60°
故选 A.
 解:连接AC,
解:连接AC,∵BD为AC的垂直平分线,
∴FA=FC,
∵四边形ABCD是正方形,
∴AD=DC=AB,
在△DCF和△DAF中,
|
∴△DCF≌△DAF,
∵三角形ABE是等边三角形,
∴AE=AB=AD,
在△DAF和△EAF中,
|
∴△DAF≌△EAF,
∴△DCF≌△DAF≌△EAF,
得:∠DFC=∠AFD=∠AFE,
又∵∠DFC+∠AFD+∠AFE=180°
∴∠DFC=∠AFD=∠AFE=60°
故选 A.
点评:本题考查了正方形各边长相等的性质,考查了正三角形各边长相等的性质,本题中求证△DCF≌△DAF≌△EAF是解题的关键.

练习册系列答案
 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
 13、如图,以直角△ABC的三边向外作正方形,其面积分别为S1,S2,S3且S1=4,S2=8,则S3=
13、如图,以直角△ABC的三边向外作正方形,其面积分别为S1,S2,S3且S1=4,S2=8,则S3=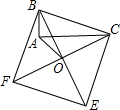 如图,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO,如果AB=4,AO=6
如图,以Rt△ABC的斜边BC为一边在△ABC的同侧作正方形BCEF,设正方形的中心为O,连接AO,如果AB=4,AO=6 如图,以Rt△ABC的斜边BC为一边作正方形BCDE,设正方形的中心为O,连接AO,如果AB=3,AO=
如图,以Rt△ABC的斜边BC为一边作正方形BCDE,设正方形的中心为O,连接AO,如果AB=3,AO= 如图,以Rt△ABC的斜边和一直角边为边长向外作正方形,面积分别为169和25,则另一直角边的长度BC为( )
如图,以Rt△ABC的斜边和一直角边为边长向外作正方形,面积分别为169和25,则另一直角边的长度BC为( ) 如图,以Rt△ABC各边为边长的正方形面积分别为S1、S2、S3,且S1+S2+S3=50,则AB=( )
如图,以Rt△ABC各边为边长的正方形面积分别为S1、S2、S3,且S1+S2+S3=50,则AB=( )