题目内容
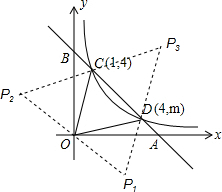
如图,一次函数y=ax+b的图象与反比例函数y=
的图象交于C,D两点,与坐标轴交于A、B两点,连结OC,OD(O是坐标原点).
(1)利用图中条件,求反比例函数的解析式和m的值;
(2)利用图中条件,求出一次函数的解析式;
(3)如图,写出当x取何值时,一次函数值小于反比例函数值?
(4)坐标平面内是否存在点P,使以O、D、P、C为顶点的四边形是平行四边形?若存在,直接写出P点的坐标;若不存在,说明理由.

| k |
| x |
(1)利用图中条件,求反比例函数的解析式和m的值;
(2)利用图中条件,求出一次函数的解析式;
(3)如图,写出当x取何值时,一次函数值小于反比例函数值?
(4)坐标平面内是否存在点P,使以O、D、P、C为顶点的四边形是平行四边形?若存在,直接写出P点的坐标;若不存在,说明理由.

(1)∵一次函数y=ax+b的图象与反比例函数y=
的图象交于C,D两点,且点C(1,4),
∴k=xy=1×4=4,
∴反比例函数的解析式为:y=
;
当x=4时,m=y=
=1,
∴m=1;
 (2)∵C(1,4),D(4,1),
(2)∵C(1,4),D(4,1),
∴
,
解得:
,
∴一次函数的解析式为:y=-x+5;
(3)结合图象的可得:当0<x<1或x>4是,一次函数值小于反比例函数值;
(4)存在.
如图,∵点C的坐标为:(1,4),点D的坐标为;(4,1),
∴直线OC的解析式为:y=4x,直线OD的解析式为:y=
x,
∵使以O、D、P、C为顶点的四边形是平行四边形,
∴直线P1P2的解析式为:y=-x①,直线P1P3的解析式为:y=4x-15②,直线P2P3的解析式为:y=
x+
③,
联立①②得:
,联立①③得:
,联立②③得:
,
∴P1(3,-3);P2(-3,3);P3(5,5).
| k |
| x |
∴k=xy=1×4=4,
∴反比例函数的解析式为:y=
| 4 |
| x |
当x=4时,m=y=
| 4 |
| 4 |
∴m=1;
 (2)∵C(1,4),D(4,1),
(2)∵C(1,4),D(4,1),∴
|
解得:
|
∴一次函数的解析式为:y=-x+5;
(3)结合图象的可得:当0<x<1或x>4是,一次函数值小于反比例函数值;
(4)存在.
如图,∵点C的坐标为:(1,4),点D的坐标为;(4,1),
∴直线OC的解析式为:y=4x,直线OD的解析式为:y=
| 1 |
| 4 |
∵使以O、D、P、C为顶点的四边形是平行四边形,
∴直线P1P2的解析式为:y=-x①,直线P1P3的解析式为:y=4x-15②,直线P2P3的解析式为:y=
| 1 |
| 4 |
| 15 |
| 4 |
联立①②得:
|
|
|
∴P1(3,-3);P2(-3,3);P3(5,5).

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目