题目内容
对于任意的实数a、b、c、d,有如下运算a↑b→c↑d=ac-bd,已知2↑4→x↑(5-3x)<0,则x的取值范围 ________.
x<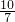
分析:首项根据新定义运算法则求得关于x的一元一次不等式,然后解不等式即可.
解答:∵a↑b→c↑d=ac-bd,
∴2↑4→x↑(5-3x)=2x-4(5-3x)=14x-20,即2↑4→x↑(5-3x)=14x-20,
∴由2↑4→x↑(5-3x)<0,得
14x-20<0,
移项,得
14x<20,
不等式的两边同时除以14,得
x<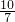 ;
;
故答案为:x<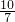 .
.
点评:本题考查了一元一次不等式的解法.解答此题的关键是弄懂新定义的运算法则,根据此运算法则列出关于x的一元一次不等式.解不等式要依据不等式的基本性质:(1)不等式的两边同时加上或减去同一个数或整式不等号的方向不变;
(2)不等式的两边同时乘以或除以同一个正数不等号的方向不变;(3)不等式的两边同时乘以或除以同一个负数不等号的方向改变.
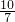
分析:首项根据新定义运算法则求得关于x的一元一次不等式,然后解不等式即可.
解答:∵a↑b→c↑d=ac-bd,
∴2↑4→x↑(5-3x)=2x-4(5-3x)=14x-20,即2↑4→x↑(5-3x)=14x-20,
∴由2↑4→x↑(5-3x)<0,得
14x-20<0,
移项,得
14x<20,
不等式的两边同时除以14,得
x<
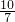 ;
;故答案为:x<
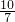 .
.点评:本题考查了一元一次不等式的解法.解答此题的关键是弄懂新定义的运算法则,根据此运算法则列出关于x的一元一次不等式.解不等式要依据不等式的基本性质:(1)不等式的两边同时加上或减去同一个数或整式不等号的方向不变;
(2)不等式的两边同时乘以或除以同一个正数不等号的方向不变;(3)不等式的两边同时乘以或除以同一个负数不等号的方向改变.

练习册系列答案
 一线名师权威作业本系列答案
一线名师权威作业本系列答案
相关题目