题目内容
【题目】如图1,两块直角三角纸板(Rt△ABC和Rt△BDE)按图所示的方式摆放(重合点为B),其中∠BDE=∠ACB=90°,∠ABC=30°,BD=DE=AC=2.将△BDE绕着点B顺时针旋转.
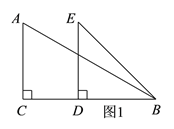
(1)当点D在BC上时,求CD的长;
(2)当△BDE旋转到A,D,E三点共线时,求△CDE的面积;
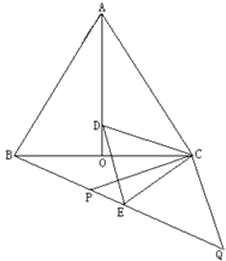
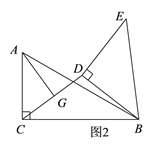
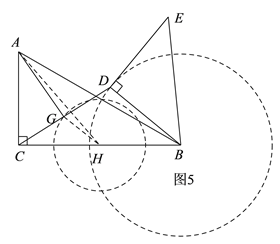
(3)如图2,连接CD,点G是CD的中点,连接AG,求AG的最大值和最小值.
【答案】(1)![]() ;(2)△CDE的面积为1或2;(3)
;(2)△CDE的面积为1或2;(3)![]() ,
,![]() .
.
【解析】分析:
(1)由已知条件易得AB=2AC=4结合AC=2及∠ACB=90°可得BC=![]() ,由此可得CD=BC-BD=
,由此可得CD=BC-BD=![]() ;
;
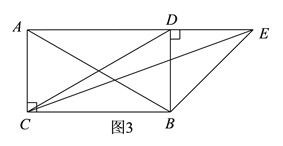
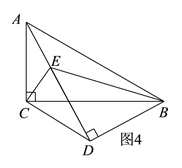
(2)根据题意分以下两种情况,画出图形,结合已知条件分析计算即可:①点D在BC上方,如图3;②点D在BC下方,如图4;
(3)如图5,取BC的中点H,连接GH、AH,由已知条件易得AH=![]() ,GH=
,GH=![]() BD=1,由题意和图可知:点G在以点H为圆心,GH为半径的⊙H上运动,点D在以B为圆心,BD为半径的⊙B上运动,由此即可得到AG的最大值和最小值.
BD=1,由题意和图可知:点G在以点H为圆心,GH为半径的⊙H上运动,点D在以B为圆心,BD为半径的⊙B上运动,由此即可得到AG的最大值和最小值.
详解:
(1)∵在△ABC中,AC=2,∠ACB=90°,∠ABC=30°,
∴AB=2AC=4,
∴BC=![]() ;
;
∵BD=2,点D在BC上,
∴CD=BC-BD=![]() ;
;
(2)①如图3,当点D在BC上方,A、D、E三点共线时,
∵A、D、E三点共线,∠BDE=90°,
∴∠ADE=90°=∠ACB,
又∵AB=BA,AC=BD,
∴△ABC≌△BAD,
∴AD=BC,
∴四边形ACBD是平行四边形,
又∵∠ACB=90°,
∴四边形ACBD是矩形,
∴![]() ;
;
②如图4,当点D在BC下方,A、D、E三点共线时,
∵BD=DE=AC,
∴∠BAD=∠ABC=30°,所以∠CAD=∠CBD=30°,
∵△ABC和△ABD中,∠ACB=∠ADB=90°,
∴A、C、D、B四点共圆,
∴∠BCD=∠ADC=30°,
∴∠BCD=∠CBD,
∴CD=DE=BD=2,
∴![]() ,
,
综上所述△CDE的面积为1或2;
(3)如图5,由题意可知,随着△BDE绕着点B进行顺时针旋转,点D的运动路线是以点B为圆心,BD为半径的圆,取BC的中点H,连接GH,AH,
∴CH=![]() BC=
BC=![]() ,
,
∴AH=![]() ,
,
∴GH是△BCD的中位线,
∴GH=![]() BD=1,
BD=1,
∴点G的运动路线是以H为圆心,1为半径的圆,
∴AG的最大值=AH+1=![]() +1,AG的最小值=AH-1=
+1,AG的最小值=AH-1=![]() -1.
-1.

 优百分课时互动系列答案
优百分课时互动系列答案 开心蛙状元作业系列答案
开心蛙状元作业系列答案【题目】某数学兴趣小组在用黑色围棋进行摆放图案的游戏中,一同学摆放了如下图案,请根据图中信息完成下列的问题:
 ...
...
(1)填写下表:
图形编号 | ① | ② | ③ | … | … |
图中棋子的总数 | ________ | ________ | ________ | … | … |
(2)第10个图形中棋子为________颗围棋;
(3)该同学如果继续摆放下去,那么第![]() 个图案要用________颗围棋;
个图案要用________颗围棋;