题目内容
（2013•聊城）如图，在等边△ABC中，AB=6，D是BC的中点，将△ABD绕点A旋转后得到△ACE，那么线段DE的长度为3
| 3 |
3
．| 3 |
分析：首先，利用等边三角形的性质求得AD=3
；然后根据旋转的性质、等边三角形的性质推知△ADE为等边三角形，则DE=AD．
| 3 |
解答：解：如图，∵在等边△ABC中，∠B=60°，AB=6，D是BC的中点，
∴AD⊥BD，∠BAD=∠CAD=30°，
∴AD=ABcos30°=6×
=3
．
根据旋转的性质知，∠EAC=∠DAB=30°，AD=AE，
∴∠DAE=∠EAC+∠CAD=∠EAC+∠BAD=60°，
∴△ADE的等边三角形，
∴DE=AD=3
，即线段DE的长度为3
．
故答案是：3
．
∴AD⊥BD，∠BAD=∠CAD=30°，
∴AD=ABcos30°=6×
| ||
| 2 |
| 3 |
根据旋转的性质知，∠EAC=∠DAB=30°，AD=AE，
∴∠DAE=∠EAC+∠CAD=∠EAC+∠BAD=60°，
∴△ADE的等边三角形，
∴DE=AD=3
| 3 |
| 3 |
故答案是：3
| 3 |
点评：本题考查了旋转的性质、等边三角形的性质．旋转的性质：旋转前后的两个图形全等，对应点与旋转中心的连线段的夹角等于旋转角，对应点到旋转中心的距离相等．
练习册系列答案
小学课堂作业系列答案
金博士一点全通系列答案
相关题目
（2013•聊城）如图，D是△ABC的边BC上一点，已知AB=4，AD=2．∠DAC=∠B，若△ABD的面积为a，则△ACD的面积为（ ）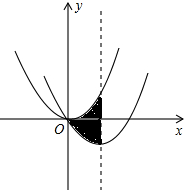
（2013•聊城）如图，在平面直角坐标系中，抛物线y=
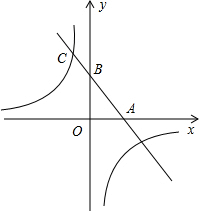（2013•聊城）如图，一次函数的图象与x轴，y轴分别相交于A，B两点，且与反比例函数y=
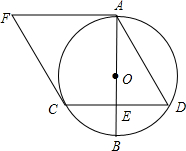（2013•聊城）如图，AB是⊙O的直径，AF是⊙O切线，CD是垂直于AB的弦，垂足为E，过点C作DA的平行线与AF相交于点F，CD=