题目内容
【题目】如图,在△ABC中,三个顶点的坐标分别为A(﹣5,0),B(4,0),C(2,5),将△ABC沿x轴正方向平移2个单位长度,再沿y轴沿负方向平移1个单位长度得到△EFG.
(1)求△EFG的三个顶点坐标.
(2)求△EFG的面积.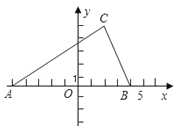
【答案】解:(1)如下图:E(﹣3,﹣1)、F(6,﹣1)、G(4,4);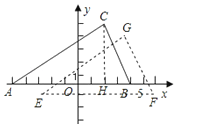
(2)如上图,过C作CH⊥AB.
∵△EFG是由△ABC沿x轴正方向平移2个单位长度,再沿y轴沿负方向平移1个单位长度得到的.
∴△EFG≌△ABC,
∴S△EFG=S△ABC ,
∵AB=|4﹣(﹣5)|=9,
CH=|5﹣0|=5,
∴S△ABC=![]() ABCH
ABCH
=![]() ×9×5
×9×5
=![]() ;
;
即S△EFG=S△ABC=![]() .
.
【解析】(1)按照题目要求,画出平移后的三角形,即可得出△EFG的三点坐标,或根据平移公式也可直接得出平移后三角形的三个顶点坐标;
(2)根据已知条件,△EFG≌△ABC,所以有S△EFG=S△ABC , 只需求出S△ABC即可,根据三角形的面积公式,易知底边AB的长度,高为点C到AB的距离,即为点C的纵坐标.
【考点精析】根据题目的已知条件,利用三角形的面积的相关知识可以得到问题的答案,需要掌握三角形的面积=1/2×底×高.

练习册系列答案
相关题目
