题目内容
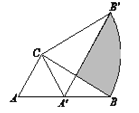
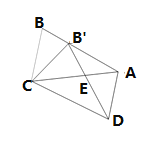
【题目】如图，等腰△ABC的顶角∠A=36°，若将其绕点C顺时针旋转36°，得到△
，点B′在AB边上，
交AC于E，连接AA′．有下列结论：①△ABC≌△；②四边形
是平行四边形；③图中所有的三角形都是等腰三角形；其中正确的结论是（ ）
A.①②B.① ③C.②③D.① ② ③
【答案】D
【解析】
①根据旋转的性质可知
则△ABC≌△
；
②根据全等的性质和三角形内角和定理即可得出
，根据内错角相等，两直线平行得出
，再根据
得出
，即可证明四边形
是平行四边形；
③根据等腰三角形的判定逐一对图中所有的三角形进行验证即可得出答案．
根据旋转的性质可知
∴△ABC≌△（SSS）；故①正确；
四边形是平行四边形，故②正确；
∴
是等腰三角形
∴
是等腰三角形
∴
是等腰三角形
∴
是等腰三角形
∴
是等腰三角形
∴
是等腰三角形
∴
是等腰三角形
∴
是等腰三角形
∴
是等腰三角形
∴
是等腰三角形
∴所有的三角形都是等腰三角形，故③正确．
故选：D．
练习册系列答案
相关题目
