题目内容
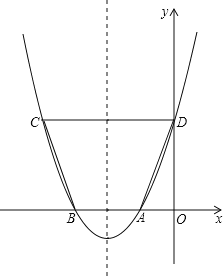
【题目】如图，抛物线y＝ax2+bx+c（a≠0）与x轴交于点（﹣3，0），其对称轴为直线x＝﹣
，结合图象分析下列结论：①abc＞0；②3a+c＞0；③当x＜0时，y随x的增大而增大：④若m，n（m＜n）为方程a（x+3）（x﹣2）+3＝0的两个根，则m＜﹣3且n＞2；⑤
＜0，其中正确的结论有（ ）
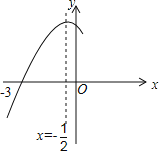
A.2个B.3个C.4个D.5个
【答案】C
【解析】
根据题意和函数图象中的数据，利用二次函数的性质可以判断各个小题中的结论是否正确，从而可以解答本题．
∵抛物线y=ax2+bx+c(a≠0)与x轴交于点(﹣3，0)，其对称轴为直线x
，
∴抛物线y=ax2+bx+c(a≠0)与x轴交于点(﹣3，0)和(2，0)，且
，
∴a=b，
由图象知：a＜0，c＞0，b＜0，
∴abc＞0，故结论①正确；
∵抛物线y=ax2+bx+c(a≠0)与x轴交于点(﹣3，0)，
∴9a﹣3b+c=0．
∵a=b，
∴c=﹣6a，
∴3a+c=﹣3a＞0，
故结论②正确；
∵当x
时，y随x的增大而增大；当
x＜0时，y随x的增大而减小，
故结论③错误；
∵抛物线y=ax2+bx+c(a≠0)与x轴交于点(﹣3，0)和(2，0)，
∴y=ax2+bx+c=a(x+3)(x﹣2)．
∵m，n(m＜n)为方程a(x+3)(x﹣2)+3=0的两个根，
∴m，n(m＜n)为方程a(x+3)(x﹣2)=﹣3的两个根，
∴m，n(m＜n)为函数y=a(x+3)(x﹣2)与直线y=﹣3的两个交点的横坐标，
结合图象得：m＜﹣3且n＞2，
故结论④成立；
∵当x时，y
0，
∴
0．
故结论⑤正确．
故选：C．
阅读快车系列答案
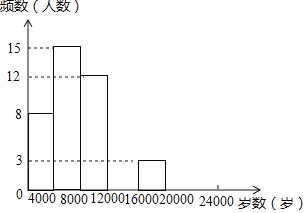
【题目】现今“微信运动”被越来越多的人关注和喜爱，某兴趣小组随机调查了我市50名教师某日“微信运动”中的步数情况进行统计整理，绘制了如下的统计图表（不完整）：
步数 | 频数 | 频率 |
0≤x＜4000 | 8 | a |
4000≤x＜8000 | 15 | 0.3 |
8000≤x＜12000 | 12 | b |
12000≤x＜16000 | c | 0.2 |
16000≤x＜20000 | 3 | 0.06 |
20000≤x＜24000 | d | 0.04 |
请根据以上信息，解答下列问题：
（1）写出a，b，c，d的值并补全频数分布直方图；
（2）本市约有37800名教师，用调查的样本数据估计日行走步数超过12000步（包含12000步）的教师有多少名？
（3）若在50名被调查的教师中，选取日行走步数超过16000步（包含16000步的两名教师与大家分享心得，求被选取的两名教师恰好都在20000步（包含20000步）以上的概率．
