题目内容
图①是一瓷砖的图案,用这种瓷砖铺设地面,图②铺成了一个2×2的近似正方形,其中完整菱形共有5个;若铺成3×3的近似正方形图案③,其中完整的菱形有13个;铺成 4×4的近似正方形图案④,其中完整的菱形有25个;如此下去,可铺成一个n×n的近似正方形图案.当得到完整的菱形共181个时,n的值为
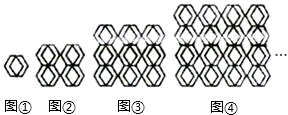
- A.7
- B.8
- C.9
- D.10
D
分析:观察图形特点,从中找出数字规律,图①菱形数为,2×12-2×1+1=1,图②为,2×22-2×2+1=5,图③为,2×32-2×3+1=13,图④为,2×42-2×4+1=25,…,据此规律可表示出图n的菱形数,由已知得到关于n的方程,从求出n的值.
解答:由已知通过观察得:
图①菱形数为,2×12-2×1+1=1,
图②为,2×22-2×2+1=5,
图③为,2×32-2×3+1=13,
图④为,2×42-2×4+1=25,
…,
所以铺成一个n×n的近似正方形图案的菱形个数为:
2n2-2n+1,
则2n2-2n+1=181,
解得:n=10或n=-9(舍去),
故选:D.
点评:此题考查的知识点是图形数字的变化类问题,解题的关键是先观察分析总结出规律,根据规律列方程求解.
分析:观察图形特点,从中找出数字规律,图①菱形数为,2×12-2×1+1=1,图②为,2×22-2×2+1=5,图③为,2×32-2×3+1=13,图④为,2×42-2×4+1=25,…,据此规律可表示出图n的菱形数,由已知得到关于n的方程,从求出n的值.
解答:由已知通过观察得:
图①菱形数为,2×12-2×1+1=1,
图②为,2×22-2×2+1=5,
图③为,2×32-2×3+1=13,
图④为,2×42-2×4+1=25,
…,
所以铺成一个n×n的近似正方形图案的菱形个数为:
2n2-2n+1,
则2n2-2n+1=181,
解得:n=10或n=-9(舍去),
故选:D.
点评:此题考查的知识点是图形数字的变化类问题,解题的关键是先观察分析总结出规律,根据规律列方程求解.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

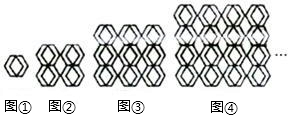
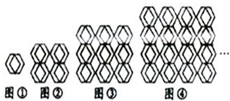 图①是一瓷砖的图案,用这种瓷砖铺设地面,图②铺成了一个2×2的近似正方形,其中完整菱形共有5个;若铺成3×3的近似正方形图案③,其中完整的菱形有13个;铺成4×4的近似正方形图案④,其中完整的菱形有25个;如此下去,可铺成一个n×n的近似正方形图案.当得到完整的菱形共221个时,n的值为( )
图①是一瓷砖的图案,用这种瓷砖铺设地面,图②铺成了一个2×2的近似正方形,其中完整菱形共有5个;若铺成3×3的近似正方形图案③,其中完整的菱形有13个;铺成4×4的近似正方形图案④,其中完整的菱形有25个;如此下去,可铺成一个n×n的近似正方形图案.当得到完整的菱形共221个时,n的值为( )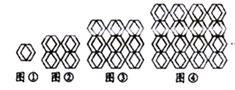
 的近似正方形图案.当得到完整的菱形共221个时,n的值为( )
的近似正方形图案.当得到完整的菱形共221个时,n的值为( )