题目内容
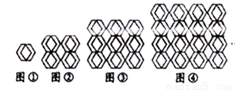
图①是一瓷砖的图案，用这种瓷砖铺设地面，图②铺成了一个2×2的近似正方形，其中完整菱形共有5个；若铺成3×3的近似正方形图案③，其中完整的菱形有13个；铺成4×4的近似正方形图案④，其中完整的菱形有25个;如此下去，可铺成一个
的近似正方形图案.当得到完整的菱形共221个时，n的值为（ ）
A.12 B.11 C.10 D.9
B
解析:分析可得：组成大正方形的每个小正方形上有一个完整的菱形，因此菱形的数目是大正方形边长的平方，即为n2；又每四个小正方形组成一个完整的菱形，这样的菱形的个数是大正方形边长减1的平方，即为（n-1）2，∴若这样铺成一个n×n的正方形图案，所得到的完整菱形的个数共有：n2+（n-1）2．即n2+（n-1）2=221，得n=11,故选B.
练习册系列答案
相关题目
图①是一瓷砖的图案，用这种瓷砖铺设地面，图②铺成了一个2×2的近似正方形，其中完整菱形共有5个；若铺成3×3的近似正方形图案③，其中完整的菱形有13个；铺成4×4的近似正方形图案④，其中完整的菱形有25个；如此下去，可铺成一个n×n的近似正方形图案．当得到完整的菱形共221个时，n的值为（ ）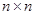
的近似正方形图案.当得到完整的菱形共221个时，n的值为（ ）