��Ŀ����
����Ŀ��ƽ��ֱ������ϵ�У�ƽ���ı���ABOC��ͼ���ã���A��C������ֱ�Ϊ��0��3��������1��0��������ƽ���ı����Ƶ�O˳ʱ����ת90�㣬�õ�ƽ���ı���A'B'OC'��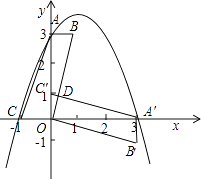
��1���������߹���C��A��A'����������ߵĽ���ʽ��
��2����ƽ���ı���ABOC��ƽ���ı���A'B'OC'�ص����֡�OC'D���ܳ���
��3����M�ǵ�һ�������������ϵ�һ���㣬�ʣ���M�ںδ�ʱ����AMA'���������������Ƕ��٣��������ʱM�����꣮
���𰸡�
��1���⣺��A��B��O��C����ABOC��ת�õ�����A������Ϊ��0��3������
��A���������3��0����
�������ߵĽ���ʽΪy=ax2+bx+c��
��A��A��C��������룬��
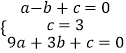 ��
��
��� 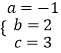 ��
��
�����ߵĽ���ʽy=��x2+2x+3
��2���⣺��AB��OC��
���OAB=��AOC=90�㣬
��OB= ![]() =
= ![]() ��
��
�֡�OC��D=��OCA=��B����C��OD=��BOA��
���C��OD�ס�BOA����OC��=OC=1��
�� ![]() =
= ![]() =
= ![]() ��
��
�֡�ABO���ܳ�Ϊ4+ ![]() ��
��
���C��OD���ܳ�Ϊ ![]() =1+
=1+ ![]()
��3���⣺
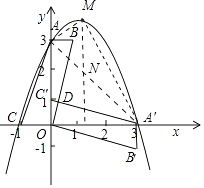
��MN��x�ύAA����N�㣬
��M��m����m2+2m+3����
AA��Ľ���ʽΪy=��x+3��N������Ϊ��m����m+3����MN�ij�Ϊ��m2+3m��
S��AMA��= ![]() MNxA��=
MNxA��= ![]() ����m2+3m����3
����m2+3m����3
=�� ![]() ��m2��3m��=��
��m2��3m��=�� ![]() ��m��
��m�� ![]() ��2+
��2+ ![]() ��
��
��0��m��3���൱m= ![]() ʱ����m2+2m+3=
ʱ����m2+2m+3= ![]() ��M��
��M�� ![]() ��
�� ![]() ����
����
��AMA�����������ֵ ![]()
����������1��������ת�����ʣ��ɵ�A��㣬���ݴ���ϵ�������ɵô𰸣���2���������������ε��ж������ʣ��ɵô𰸣���3����������ĺͲ�ɵö��κ��������ݶ��κ��������ʣ��ɵô𰸣�
�����㾫����������Ҫ�����˶��κ��������ʵ����֪ʶ�㣬��Ҫ���������ԣ���a>0ʱ���Գ�����ߣ�y��x�������С���Գ����ұߣ�y��x���������a<0ʱ���Գ�����ߣ�y��x��������Գ����ұߣ�y��x�������С������ȷ�����⣮

 ��������״Ԫ��ϵ�д�
��������״Ԫ��ϵ�д� �ƸԿ�����ҵ��ϵ�д�
�ƸԿ�����ҵ��ϵ�д� ��Ԫ����ĩ��ϰ�ȷ��ϵ�д�
��Ԫ����ĩ��ϰ�ȷ��ϵ�д�