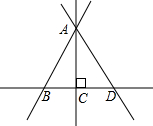题目内容
已知，∠AOB=25°，OC⊥OA，OD⊥OB，则∠COD等于（ ）
| A．25° | B．115° | C．155° | D．25°或155° |
∵OC⊥OA，OD⊥OB，
∴∠AOC=90°，∠BOD=90°．
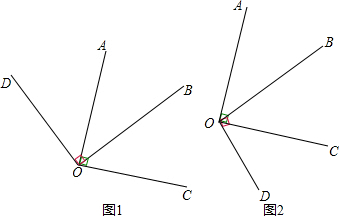
如图1，∠AOD=∠BOD-∠AOB=90°-25°=65°，
则∠COD=∠AOD+∠AOC=65°+90°=155°；
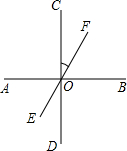
如图2，∠BOC=∠AOC-∠AOB=90°-25°=65°，
∠COD=∠BOD-∠BOC=90°-65°=25°．
综上所述，∠COD等于155°或25°．
故选D．
∴∠AOC=90°，∠BOD=90°．
如图1，∠AOD=∠BOD-∠AOB=90°-25°=65°，
则∠COD=∠AOD+∠AOC=65°+90°=155°；
如图2，∠BOC=∠AOC-∠AOB=90°-25°=65°，
∠COD=∠BOD-∠BOC=90°-65°=25°．
综上所述，∠COD等于155°或25°．
故选D．
练习册系列答案
导学全程练创优训练系列答案
相关题目
