题目内容
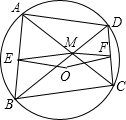 已知:如图,⊙O的内接四边形ABCD的对角线交于点M,点E、F分别为AB、CD的中点.
已知:如图,⊙O的内接四边形ABCD的对角线交于点M,点E、F分别为AB、CD的中点.
求证:∠OEM=∠OFM.
证明:∵E、F分别是AB、CD的中点,
∴OE⊥AB,OF⊥CD,且BE= AB,CF=
AB,CF= DC
DC
又∵∠ABD=∠DCA,∠BAC=∠CDB,
∴△ABM∽△DCM.
∴ =
= .
.
∴ =
= =
= =
=
又∵∠EBM=∠FCM,
∴△EBM∽△FCM.
∴∠MEB=∠MFC.
而∠OEB=∠OFC=90°
∴∠OEM=∠MEB-∠OEB=∠MFC-∠OFC=∠OEM,即∠OEM=∠OFM.
分析:先证△ABM∽△DCM(AA),根据相似三角形的对应边成比例求得 =
= ;然后根据垂径定理推知
;然后根据垂径定理推知 =
= =
= =
= ;然后推知△EBM∽△FCM,根据对应角∠MEB=∠MFC;最后根据图示中的角与角间的关系证明∠OEM=∠OFM.
;然后推知△EBM∽△FCM,根据对应角∠MEB=∠MFC;最后根据图示中的角与角间的关系证明∠OEM=∠OFM.
点评:本题综合考查了圆周角定理、相似三角形的判定与性质.解答该题的关键是根据垂径定理求得BE= AB,CF=
AB,CF= DC.
DC.
∴OE⊥AB,OF⊥CD,且BE=
 AB,CF=
AB,CF= DC
DC又∵∠ABD=∠DCA,∠BAC=∠CDB,
∴△ABM∽△DCM.
∴
 =
= .
.∴
 =
= =
= =
=
又∵∠EBM=∠FCM,
∴△EBM∽△FCM.
∴∠MEB=∠MFC.
而∠OEB=∠OFC=90°
∴∠OEM=∠MEB-∠OEB=∠MFC-∠OFC=∠OEM,即∠OEM=∠OFM.
分析:先证△ABM∽△DCM(AA),根据相似三角形的对应边成比例求得
 =
= ;然后根据垂径定理推知
;然后根据垂径定理推知 =
= =
= =
= ;然后推知△EBM∽△FCM,根据对应角∠MEB=∠MFC;最后根据图示中的角与角间的关系证明∠OEM=∠OFM.
;然后推知△EBM∽△FCM,根据对应角∠MEB=∠MFC;最后根据图示中的角与角间的关系证明∠OEM=∠OFM.点评:本题综合考查了圆周角定理、相似三角形的判定与性质.解答该题的关键是根据垂径定理求得BE=
 AB,CF=
AB,CF= DC.
DC. 
练习册系列答案
相关题目
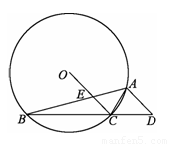
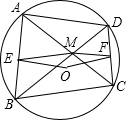 已知:如图,⊙O的内接四边形ABCD的对角线交于点M,点E、F分别为AB、CD的中点.
已知:如图,⊙O的内接四边形ABCD的对角线交于点M,点E、F分别为AB、CD的中点.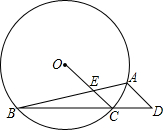 OC交AB于E.
OC交AB于E.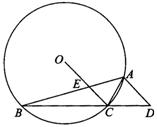
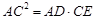 ;
;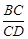 的值。
的值。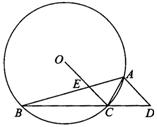
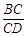 的值.
的值.