题目内容
已知:如图,⊙O的内接△ABC中,∠BAC=45°,∠ABC=15°,AD∥OC并交BC的延长线于D,OC交AB于E.
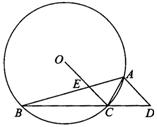
1.求∠D的度数;
2.求证:AC2=AD·CE;
3.求![]() 的值.
的值.
1.解:如图,连结OB.

∵⊙O的内接△ABC中,∠BAC=45°,
∴∠BOC=2∠BAC=90°.
∵OB=OC,
∴∠OBC=∠OCB=45°.
∵AD∥OC,
∴∠D=∠OCB=45°.
2.证明:∵∠BAC=45°,∠D=45°,
∴∠BAC=∠D.
∵AD∥OC,
∴∠ACE=∠DAC.
∴△ACE∽△DAC.

∴AC2=AD·CE.
3.解法一:如图,延长BO交DA的延长线于F,连结OA.
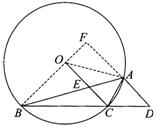
∵AD∥OC,
∴∠F=∠BOC=90°.
∵∠ABC=15°,
∴∠OBA=∠OBC-∠ABC=30°.
∵OA=OB.
∴∠FOA=∠OBA+∠OAB=60°,∠OAF=30°.
∴![]() .
.
∵AD∥OC,
∴△BOC∽△BFD.
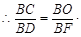
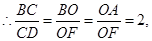 即
即![]() 的值为2.
的值为2.
解法二:作OM⊥BA于M,设⊙O的半径为r,可得![]()
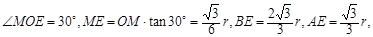
所以![]()
解析:略

练习册系列答案
相关题目
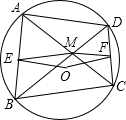 已知:如图,⊙O的内接四边形ABCD的对角线交于点M,点E、F分别为AB、CD的中点.
已知:如图,⊙O的内接四边形ABCD的对角线交于点M,点E、F分别为AB、CD的中点.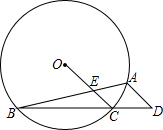 OC交AB于E.
OC交AB于E.
 ;
; 的值。
的值。
 的值.
的值.