题目内容
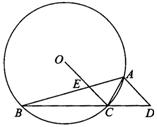
已知:如图,⊙O的内接△ABC中,∠BAC=45°,∠ABC =15°,AD∥OC并交BC的延长线于D,OC交AB于E。
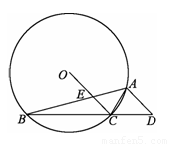
1.(1)求∠D的度数;
2.(2)求证: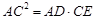 ;
;
3.(3)求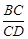 的值。
的值。
【答案】
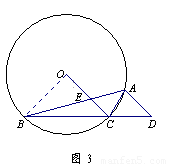
1.(1)解:如图3,连结OB。- - - - - - - 1分
∵ ⊙O的内接△ABC中,∠BAC=45°,
∴ ∠BOC =2∠BAC =90°。
∵ OB=OC ,
∴ ∠OBC =∠OCB =45°。
∵ AD∥OC ,
∴ ∠D =∠OCB =45°。 - - - - - - - - - - - -2分
2.(2)证明:∵ ∠BAC =45°,∠D =45°,
∴ ∠BAC =∠D 。 - - - - - - - - - - - - - 3分
∵ AD∥OC ,
∴ ∠ACE =∠DAC 。 - - - - - - - - - - - -4分
∴ △ACE ∽△DAC 。
∴ 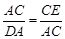 。
。
∴ 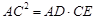 。- - - - - - - - - - - - - - 5分
。- - - - - - - - - - - - - - 5分
3.(3)解法一:如图4,延长BO交DA的延长线于F,连结OA 。
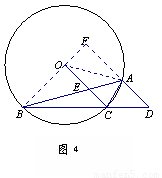
∵ AD∥OC ,
∴ ∠F=∠BOC =90°。
∵ ∠ABC =15°,
∴ ∠OBA =∠OBC -∠ABC =30°。
∵ OA = OB ,
∴ ∠FOA=∠OBA+∠OAB =60°,∠OAF =30°。
∴ 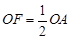 。
。
∵ AD∥OC ,
∴ △BOC ∽△BFD 。
∴ 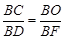 。
。
∴ 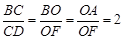 ,即
,即 的值为2。 - - - - - - - - -- - - - -7分
的值为2。 - - - - - - - - -- - - - -7分
解法二:作OM⊥BA于M,设⊙O的半径为r,可得BM=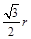 ,OM=
,OM= ,
,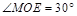 ,
, ,BE=
,BE= ,AE=
,AE= ,所以
,所以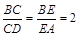
【解析】略

练习册系列答案
相关题目
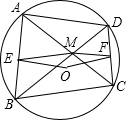 已知:如图,⊙O的内接四边形ABCD的对角线交于点M,点E、F分别为AB、CD的中点.
已知:如图,⊙O的内接四边形ABCD的对角线交于点M,点E、F分别为AB、CD的中点.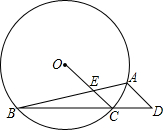 OC交AB于E.
OC交AB于E.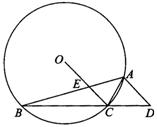
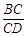 的值.
的值.