题目内容
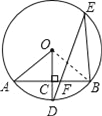
【题目】如图,AB是⊙O的一条弦,OD⊥AB,垂足为点C,交⊙O于点D,点E在⊙O上.
(1)若∠AOD=52°,求∠DEB的度数;
(2)若OC=3,OA=6,求tan∠DEB的值.

【答案】(1)∠DEB=26°;(2)tan∠DEB=![]() .
.
【解析】试题分析:(1)连接OB,根据垂径定理得出![]() ,故可得出∠BOD=∠AOD=52°,再由圆周角定理即可得出结论;
,故可得出∠BOD=∠AOD=52°,再由圆周角定理即可得出结论;
(2)根据OD⊥AB,OC=3,OA=6可得出∠OAC=30°,故∠AOC=60°,由此得出∠DEB的度数,进而可得出结论.
试题解析:(1)连接OB,
∵OD⊥AB,∴![]() ,∴∠BOD=∠AOD=52°,
,∴∠BOD=∠AOD=52°,
∴∠DEB=![]() ∠BOD=26°;
∠BOD=26°;
(2)∵OD⊥AB,OC=3,OA=6,∴OC=![]() OA,即∠OAC=30°,∴∠AOC=60°,
OA,即∠OAC=30°,∴∠AOC=60°,
∴∠DEB=![]() ∠AOC=30°,∴tan∠DEB=
∠AOC=30°,∴tan∠DEB=![]() .
.

练习册系列答案
相关题目