题目内容
【题目】已知正方形![]() ,点
,点![]() 为边
为边![]() 的中点.
的中点.
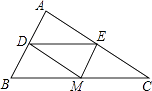
(1)如图1,点![]() 为线段
为线段![]() 上的一点,且
上的一点,且![]() ,延长
,延长![]() ,
,![]() 分别与边
分别与边![]() ,
,![]() 交于点
交于点![]() ,
,![]() .
.
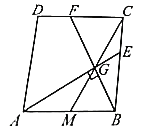
①求证:![]() ;
;
②求证:![]() .
.
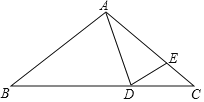
(2)如图2,在边![]() 上取一点
上取一点![]() ,满足
,满足![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() 延长交
延长交![]() 于点
于点![]() ,求
,求![]() 的值.
的值.
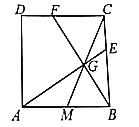
【答案】(1)详见解析;(2)![]()
【解析】
试题分析:(1)①利用ASA判定证明两个三角形全等;②先利用相似三角形的判定,再利用相似三角形的性质证明;(2)构造直角三角形,求一个角的正切值.
试题解析:(1)①证明:∵四边形![]() 为正方形,∴
为正方形,∴![]() ,
,![]() ,
,
又![]() ,∴
,∴![]() ,又
,又![]() ,∴
,∴![]() ,
,
∴![]() (ASA),∴
(ASA),∴![]() .
.
②证明:∵![]() ,点
,点![]() 为
为![]() 中点,∴
中点,∴![]() ,∴
,∴![]() ,
,
又∵![]() ,从而
,从而![]() ,又
,又![]() ,∴
,∴![]() ,
,
∴![]() ,即
,即![]() ,由
,由![]() ,得
,得![]() .
.
由①知,![]() ,∴
,∴![]() ,∴
,∴![]() .
.
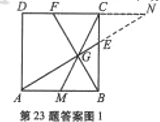
(2)解:(方法一)
延长![]() ,
,![]() 交于点
交于点![]() (如图1),由于四边形
(如图1),由于四边形![]() 是正方形,所以
是正方形,所以![]() ,
,
∴![]() ,又
,又![]() ,∴
,∴![]() ,
,
故![]() ,即
,即![]() ,
,
∵![]() ,
,![]() ,∴
,∴![]() ,由
,由![]() 知,
知,![]() ,
,
又![]() ,∴
,∴![]() ,不妨假设正方形边长为1,
,不妨假设正方形边长为1,
设![]() ,则由
,则由![]() ,得
,得![]() ,
,
解得![]() ,
,![]() (舍去),∴
(舍去),∴![]() ,
,
于是![]() ,
,
(方法二)
不妨假设正方形边长为1,设![]() ,则由
,则由![]() ,得
,得![]() ,
,
解得![]() ,
,![]() (舍去),即
(舍去),即![]() ,
,
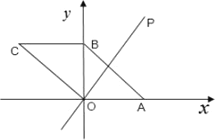
作![]() 交
交![]() 于
于![]() (如图2),则
(如图2),则![]() ,∴
,∴![]() ,
,
设![]() ,则
,则![]() ,
,![]() ,∵
,∵![]() ,即
,即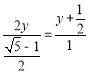 ,
,
解得![]() ,∴
,∴![]() ,从而
,从而![]() ,此时点
,此时点![]() 在以
在以![]() 为直径的圆上,
为直径的圆上,
∴![]() 是直角三角形,且
是直角三角形,且![]() ,
,
由(1)知![]() ,于是
,于是![]() .
.


练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】甲、乙、丙三位运动员在相同条件下各射靶10次,每次射靶的成绩如下:
甲:9,10,8,5,7,8,10,8,8,7;
乙:5,7,8,7,8,9,7,9,10,10;
丙:7,6,8,5,4,7,6,3,9,5.
(1)根据以上数据完成下表:
平均数 | 中位数 | 方差 | |
甲 | 8 | 8 | |
乙 | 8 | 8 | 2.2 |
丙 | 6 | 3 |
(2)依据表中数据分析,哪位运动员的成绩最稳定,并简要说明理由;
(3)比赛时三人依次出场,顺序由抽签方式决定.求甲、乙相邻出场的概率.