题目内容
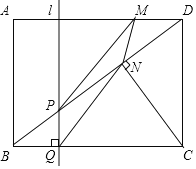
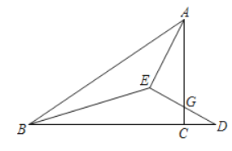
【题目】如图,在![]() 中,
中,![]() 的平分线
的平分线![]() 相交于点
相交于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]()
(1)求证:![]()
(2)当![]() 时,求
时,求![]() 的长.
的长.
【答案】(1)见解析;(2)3-![]()
【解析】
(1)利用等角的余角相等,证得∠EAG=∠D,利用AAS即可证明结论;
(2)根据勾股定理求得BC的长,再利用(1)的结论即可求解.
(1)∵BE,AE分别平分∠ABC,∠BAC的角平分线,
∴∠ABE=∠DBE,∠BAE=∠EAG,
∵DE⊥AE,
∴∠AED=90°,
∴∠EAG+∠AGE=90°,
∵∠ACB=90°,
∴∠ACD=180°-∠ACB=90°,
∴∠CGD+∠D=90°,
∵∠EGA=∠CGD,
∴∠EAG=∠D,
∴∠BAE =∠D,
在△ABE和△DBE中,
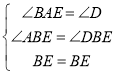 ,
,
∴△ABE≌△DBE(AAS);
(2)∵AB=3,AC=2,∠ACB=90°,
∴BC2+AC2=AB2,得:![]() ,
,
∵△ABE≌△DBE,
∴AB=BD=3,
∴CD=BD-BC=3-![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】为了解某小区居民使用共享单车次数的情况,某研究小组随机采访该小区的10位居民,得到这10位居民一周内使用共享单车的次数统计如下:
使用次数 | 0 | 5 | 10 | 15 | 20 |
人数 | 1 | 1 | 4 | 3 | 1 |
(1)这10位居民一周内使用共享单车次数的中位数是 次,众数是 次.
(2)若小明同学把数据“20”看成了“30”,那么中位数,众数和平均数中不受影响的是 .(填“中位数”,“众数”或“平均数”)
(3)若该小区有2000名居民,试估计该小区居民一周内使用共享单车的总次数.