题目内容
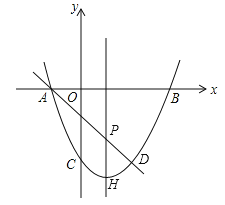
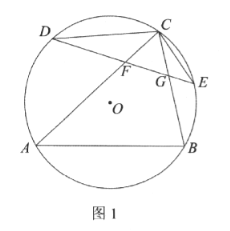
【题目】如图1,![]() 内接于
内接于![]() 分别是
分别是![]() 和
和![]() 所对弧的中点,弦
所对弧的中点,弦![]() 分别交
分别交![]() 于点
于点![]() ,连结
,连结![]()
(1)求证:![]() 是等边三角形.
是等边三角形.
(2)若![]()
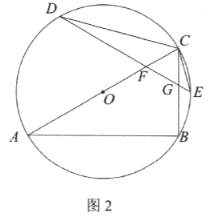
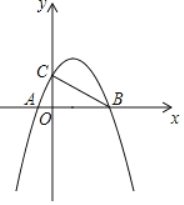
①如图2,当![]() 为
为![]() 的直径时,求
的直径时,求![]() 的长.
的长.
②当![]() 将
将![]() 的面积分成了
的面积分成了![]() 的两部分时,求
的两部分时,求![]() 的长.
的长.
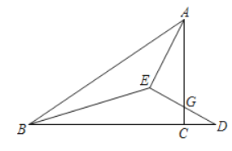
(3)连结![]() 交
交![]() 于点
于点![]() ,若
,若![]() :则
:则![]() 的值为_______. (请直接写出答案)
的值为_______. (请直接写出答案)
【答案】(1)见解析;(2)①8;②![]() 或
或![]() ;(3)
;(3)![]()
【解析】
(1)利用弧的关系证得![]() ,
,![]() ,利用三角形外角的性质证得∠CFG=60°,从而证得
,利用三角形外角的性质证得∠CFG=60°,从而证得![]() 是等边三角形;
是等边三角形;
(2)①连结OD,利用![]() 求得直径AC的长,得到半径OD=
求得直径AC的长,得到半径OD=![]() ,证得∠DOC=90°,在Rt
,证得∠DOC=90°,在Rt![]() 中,再利用
中,再利用![]() 即可求解;
即可求解;
②利用弧的关系![]() =120°=
=120°=![]() ,证得DE=AB=12,分DF:FG=2:1或DF:FG=1:2两种情况讨论,证得△DCF△CEG,利用对应边成比例分别计算即可求解;
,证得DE=AB=12,分DF:FG=2:1或DF:FG=1:2两种情况讨论,证得△DCF△CEG,利用对应边成比例分别计算即可求解;
(3)作出如图的辅助线,设![]() ,
,![]() ,得到
,得到![]() ,证得△AHD∽△BHC,△DBG∽△CEG,△DFA∽△CFE,分别求得BC、EF、EG、DF、FA的长,即可求解.
,证得△AHD∽△BHC,△DBG∽△CEG,△DFA∽△CFE,分别求得BC、EF、EG、DF、FA的长,即可求解.
(1)∵∠ACB=60°,
∴优弧![]() =120°,
=120°,
∴![]() ,
,
∵D,E分别是![]() ,
,![]() 的中点,
的中点,
∴![]() ,
,
∴∠ACD+∠EDC=60°=∠CFG,
∵∠ACB=60°,
∴△CFG是等边三角形;
(2)①连结OD,
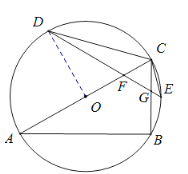
∵AC是圆O的直径,AB=12,
∴∠B=90°,
∵∠ACB=60°,
![]() ,
,
∴AC=![]() ,
,
∴OD=![]() ,
,
由(1)得:△CFG为等边三角形,
∴∠CFG=60![]() ,
,
∵点D是![]() 的中点,
的中点,
∴∠DOC=90°,
∵∠DFO=∠CFG=60°,
![]() ,
,
∴DF=8;
②由(1)得:![]() ,
,
∵D、E分别是![]() 、
、![]() 的中点,
的中点,
∴![]() =120°=
=120°=![]() ,
,
∴DE=AB=12,
ⅰ)当DF:FG=2:1时,
设FG=![]() ,DF=2
,DF=2![]() ,
,
由(1)得:△CFG为等边三角形,
∴![]() ,GE=12-3
,GE=12-3![]() ,∠CFE=60
,∠CFE=60![]() ,
,
∵![]() ,
,![]() ,
,
∴∠DCA=∠CED,∠CDE=∠ECB,
∴△DCF△CEG,
∴![]() ,
,
∴![]() ,
,
∴![]()
![]() ,
,
∴DF=![]() ,EF=12- DF=
,EF=12- DF=![]() ,
,
连结OD交AC于点M,
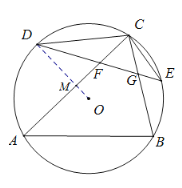
∵D是![]() 的中点,
的中点,
∴OD⊥AC,
在Rt△DMF中,∠DFM=∠CFG=60°,
∴FM=![]() DF=
DF=![]() ,
,
∴AC=2(FM+CF)= 2(![]() +
+![]() )=
)= ![]() ;
;
ⅱ)当DF:FG=1:2时,
设DF=![]() ,FG=CF=CG=2
,FG=CF=CG=2![]() ,GE=12-3
,GE=12-3![]() ,
,
同理,∴△DCF△CEG,
∴![]() ,
,
∴![]() ,
,
∴![]() =
=![]() ,
,
即DF=![]() ,EF=12- DF=
,EF=12- DF=![]() ,CF=
,CF=![]() ,
,
同理得AC=![]() ;
;
(3)作CP∥FD交BD延长线于点P,连接AD,
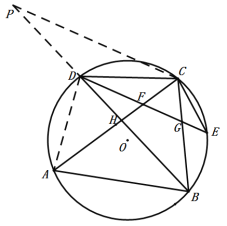
∵点D、E分别是![]() 、
、![]() 的中点,
的中点,
∴∠CDF=∠FDH,AD=DC,
∵CP∥FD,
∴∠FDC=∠DCP,∠CPD=∠FDH,![]() ,
,
∴∠DCP=∠CPD,
∴PD=CD,
∴![]() ,
,
∵![]() ,
,
∴设![]() ,
,![]() ,则
,则![]() ,
,
∴![]() ,
,
∵![]() ,∠AHD=∠BHC,
,∠AHD=∠BHC,
∴∠DAH=∠CBH,
∴△AHD∽△BHC,
∴![]() ,即
,即![]() ,
,
∴ ,
,
∴![]() ;
;
由(1)得:△CFG为等边三角形,
∴![]() ,∠CFE=60
,∠CFE=60![]() ,
,
∵![]() ,
,
∴∠HBC=∠CEF,
∴△HBC∽△CEF,
∴![]() ,即
,即 ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∵∠DBG=∠CEG,∠DGB=∠CGE,
∴△DBG∽△CEG,
∴![]() ,即
,即 ,
,
∴![]() ;
;
∴![]() ,
,
同理:∴△DFA∽△CFE,
∴![]() ,即
,即 ,
,
∴![]() ;
;
∴![]() ,
,
∴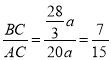 .
.
故答案为:![]() .
.