题目内容
【题目】完成下面的证明:
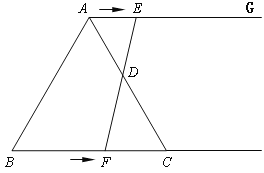
已知:如图,D是BC上任意一点,BE⊥AD,交AD的延长线于点E,CF⊥AD,垂足为F.
求证:∠1=∠2.
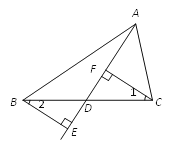
证明:∵ BE⊥AD(已知),
∴ ∠BED= °( ).
又∵ CF⊥AD(已知),
∴ ∠CFD= °.
∴ ∠BED=∠CFD(等量代换).
∴ BE∥CF( ).
∴ ∠1=∠2( ).
【答案】证明见解析
【解析】试题分析:由BE垂直于AD,利用垂直的定义得到∠BED为直角,再由CF垂直于AD,得到∠CFD为直角,得到一对内错角相等,进而确定出BE与CF平行,利用两直线平行内错角相等即可得证.
试题解析:∴∠BED=90°(垂直定义),
∵CF⊥AD,
∴∠CFD=90°,
∴∠BED=∠CFD,
∴BE∥CF(内错角相等,两直线平行),
∴∠1=∠2(两直线平行,内错角相等).
故答案为:90;垂直的定义;90;内错角相等,两直线平行;两直线平行,内错角相等

练习册系列答案
 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案
相关题目