题目内容
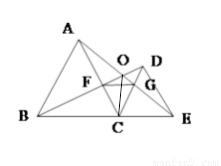
如图所示,已知△ABC和△DCE均是等边三角形,点B、C、E在同一条直线上,AE与BD交于点O,AE与CD交于点G,AC与BD交于点F,连接OC、FG,则下列结论中:①AE=BD;②AG=BF;③FG∥BE;④∠BOC=∠EOC,正确的是
【答案】
①②③④
【解析】∵△ABC和△DCE均是等边三角形,
∴BC=AC,CD=CE,∠ACB=∠ECD=60°,
∴∠ACB+∠ACD=∠ACD+∠ECD,∠ACD=60°,
∴△BCD≌△ACE(SAS),
∴AE=BD,(①正确)
∠CBD=∠CAE,
∵∠BCA=∠ACG=60°,AC=BC,
∴△BCF≌△ACG(ASA),
∴AG=BF,(②正确)
同理:△DFC≌△EGC(ASA),
∴CF=CG,
∴△CFG是等边三角形,
∴∠CFG=∠FCB=60°,
∴FG∥BE,(③正确)
过C作CM⊥AE于M,CN⊥BD于N,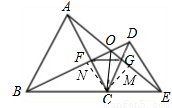
∵△BCD≌△ACE,
∴∠BDC=∠AEC,
∵CD=CE,∠CND=∠CMA=90°,
∴△CDN≌△CEM,
∴CM=CN,
∵CM⊥AE,CN⊥BD,
∴∠BOC=∠EOC,∴④正确;
故答案为:①②③④.
|

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
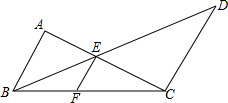 如图所示,已知AB∥EF∥CD,若AB=6厘米,CD=9厘米.求EF.
如图所示,已知AB∥EF∥CD,若AB=6厘米,CD=9厘米.求EF.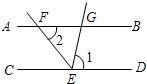 5、如图所示,已知AB∥CD,EF平分∠CEG,∠1=80°,则∠2的度数为( )
5、如图所示,已知AB∥CD,EF平分∠CEG,∠1=80°,则∠2的度数为( )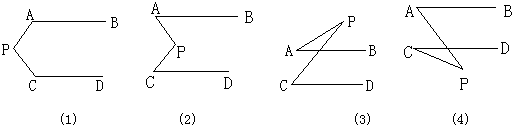
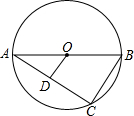 如图所示,已知AB为圆O的直径,AC为弦,OD∥BC交AC于D,OD=2cm,求BC的长.
如图所示,已知AB为圆O的直径,AC为弦,OD∥BC交AC于D,OD=2cm,求BC的长.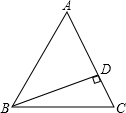 如图所示,已知AB=AC,BD⊥AC,试说明∠BAC=2∠CBD.
如图所示,已知AB=AC,BD⊥AC,试说明∠BAC=2∠CBD.