题目内容
【题目】完成下面的证明:
已知:如图.BE平分∠ABD,DE平分∠BDC,且∠1+∠2=90°.求证:AB∥CD.
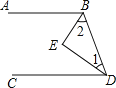
证明:∵DE平分∠BDC(已知),
∴∠BDC=2∠1(_______________).
∵BE平分∠ABD(已知),
∴∠ABD=2∠2(_____________).
∴∠BDC+∠ABD=2∠1+2∠2=2(∠1+∠2)(__________).
∵∠1+∠2=90°(已知),
∴∠ABD+∠BDC=______(__________).
∴AB∥CD(______________).
【答案】 角平分线的性质 角的平分线的性质 等量代换 180° 等量代换 同旁内角互补两直线平行
【解析】试题分析:运用角平分线的定义,结合图形可知∠ABD=2∠1,∠BDC=2∠2,又已知∠1+∠2=90°,可得同旁内角∠ABD和∠BDC互补,从而证得AB∥CD.
试题解析:
证明:
∵DE平分∠BDC(已知),
∴∠BDC=2∠1( 角平分线的性质 ).
∵BE平分∠ABD(已知),
∴∠ABD=2∠2(角的平分线的性质).
∴∠BDC+∠ABD=2∠1+2∠2=2(∠1+∠2)( 等量代换 ).
∵∠1+∠2=90°(已知),
∴∠ABD+∠BDC= 180° ( 等量代换 ).
∴AB∥CD( 同旁内角互补两直线平行 ).

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目