题目内容
【题目】如图,∠A=15°,AB=BC=CD=DE=EF,则∠DEF等于( ) 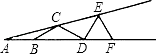
A.90°
B.75°
C.70°
D.60°
【答案】D
【解析】解:∵AB=BC=CD=DE=EF,∠A=15°, ∴∠BCA=∠A=15°,
∴∠CBD=∠BDC=∠BCA+∠A=15°+15°=30°,
∴∠BCD=180°﹣(∠CBD+∠BDC)=180°﹣60°=120°,
∴∠ECD=∠CED=180°﹣∠BCD﹣∠BCA=180°﹣120°﹣15°=45°,
∴∠CDE=180°﹣(∠ECD+∠CED)=180°﹣90°=90°,
∴∠EDF=∠EFD=180°﹣∠CDE﹣∠BDC=180°﹣90°﹣30°=60°,
∴∠DEF=180°﹣(∠EDF+∠EFC)=180°﹣120°=60°.
故选D.
根据已知条件,利用等腰三角形的性质及三角形的内角和外角之间的关系进行计算.

练习册系列答案
相关题目
【题目】已知二次函数y=ax2+bx+c中,其函数y与自变量x之间的部分对应值如下表所示:
x | … | 0 | 1 | 2 | 3 | 4 | … |
y | … | 4 | 1 | 0 | 1 | 4 | … |
点A(x1,y1)、B(x2,y2)在函数的图象上,则当1<x1<2,3<x2<4时,y1与y2的大小关系正确的是( )
A.y1>y2B.y1<y2C.y1≥y2D.y1≤y2
