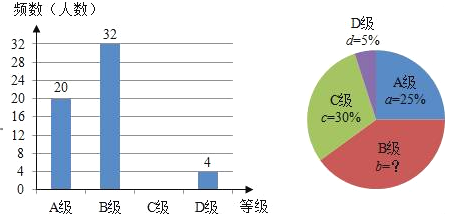
��Ŀ����
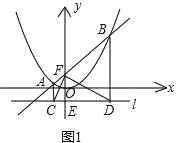
����Ŀ����֪����ͼ1������E��0��-1����ƽ����x���ֱ��l��������y=![]() x2�ϵ�����A��B�ĺ�����ֱ�Ϊ-1��4��ֱ��AB��y���ڵ�F������A��B�ֱ���ֱ��l�Ĵ��ߣ�����ֱ�Ϊ��C��D������CF��DF��
x2�ϵ�����A��B�ĺ�����ֱ�Ϊ-1��4��ֱ��AB��y���ڵ�F������A��B�ֱ���ֱ��l�Ĵ��ߣ�����ֱ�Ϊ��C��D������CF��DF��
��1�����A��B��F�����ꣻ
��2����֤��CF��DF��
��3����P��������y=![]() x2�Գ����Ҳ�ͼ���ϵ�һ���㣬����P��PQ��PO��x���ڵ�Q���Ƿ���ڵ�Pʹ����OPQ����CDF���ƣ������ڣ���������з��������ĵ�P�����ꣻ�������ڣ���˵�����ɣ�
x2�Գ����Ҳ�ͼ���ϵ�һ���㣬����P��PQ��PO��x���ڵ�Q���Ƿ���ڵ�Pʹ����OPQ����CDF���ƣ������ڣ���������з��������ĵ�P�����ꣻ�������ڣ���˵�����ɣ�

���𰸡���1��A��-1��![]() ����B��4��4������F��0��1����2��֤������������3��P1��2��1����P2��8��16��
����B��4��4������F��0��1����2��֤������������3��P1��2��1����P2��8��16��
��������
�����������1������ϵ������⼴����
��2����Rt��CEF�������DEF�߳����ù��ɶ���֤��CF��DF��
��3������������⣬�ȼ�����ڣ����Ƿ��ҵ����������ĵ�P�����꣬����������������1��Rt��QPO��Rt��CFD����2��Rt��OPQ��Rt��CFD�����ݱ������P�����꣮
�����������1����ͼ1��
��x=-1ʱ��y=![]() ����x=4ʱ��y=4
����x=4ʱ��y=4
��A��-1��![]() ����B��4��4��
����B��4��4��
��ֱ��AB�Ľ���ʽΪy=kx+b
��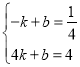 �����
�����![]()
��ֱ��AB�Ľ���ʽΪy=![]() x+1
x+1
��x=0ʱ��y=1
��F��0��1��
��2����Rt��CEF��CE=1��EF=2��
���ݹ��ɶ����ã�CF2=CE2+EF2=12+22=5��
��CF=![]()
��Rt��DEF��DE=4��EF=2
��DF2=DE2+EF2=42+22=20
��DF=2![]()
�ɣ�1����C��-1��-1����D��4��-1��
��CD=5
��CD2=52=25
��CF2+DF2=CD2
���CFD=90��
��CF��DF
��3�����ڣ���ͼ2��PM��x�ᣬ����Ϊ��M
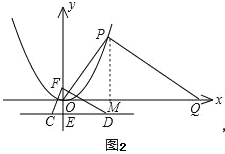
����PQ��OP
��Rt��OPM��Rt��OQP
��![]() ��
��![]()
��P��x��![]() x2����x��0����
x2����x��0����
��PM=![]() x2��OM=x
x2��OM=x
�ٵ�Rt��QPO��Rt��CFDʱ��![]()
��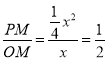
���x=2��P1��2��1��
�ڵ�Rt��OPQ��Rt��CFDʱ��![]()
��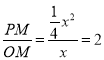
���x=8
��P2��8��16��
���ϣ����ڵ�P1��2��1����P2��8��16��ʹ����OPQ����CDF���ƣ�