题目内容
【题目】如图，在平行四边形ABCD中，AC是对角线，E是AD边上一点，连接BE交AC于点F，∠FAE=∠FEA=30°，G为AB边的中点，连接GF．
（1）如图1，若BC=
，AF=2，求△AGF的面积；
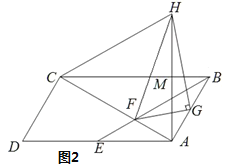
（2）如图2，过点G作GH⊥GF，连接HA交BC于点M，连接HC，且HA=HC，连接HF，求证：MC=
MH
【答案】（1）
；（2）证明见解析.
【解析】
（1）由题意作出辅助线，并利用平行四边形的性质进行分析计算；
（2）根据题意作出辅助线，并利用平行四边形的判定与性质以及全等三角形的判定与性质进行分析证明.
解：（1）
，
，
平行四边形
，
，
又
，
，
，
，
，
G为AB中点，
.
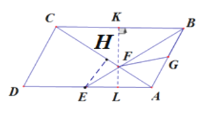
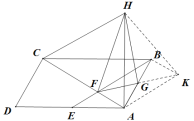
（2）延长FG到K，使GF=GK，连接AK,BK,HK,
又
，
四边形
为平行四边形，
，
，
又
，
，
，
，
，
等边
，
，
.
练习册系列答案
相关题目
