题目内容
【题目】如图,已知抛物线y=x2+bx+c与直线y=﹣x+3相交于坐标轴上的A,B两点,顶点为C.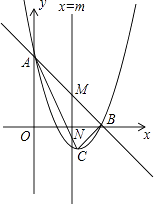
(1)填空:b= , c=;
(2)将直线AB向下平移h个单位长度,得直线EF.当h为何值时,直线EF与抛物线y=x2+bx+c没有交点?
(3)直线x=m与△ABC的边AB,AC分别交于点M,N.当直线x=m把△ABC的面积分为1:2两部分时,求m的值.
【答案】
(1)﹣4,3
(2)解:∵将直线AB:y=﹣x+3向下平移h个单位长度,得直线EF,
∴可设直线EF的解析式为y=﹣x+3﹣h.
把y=﹣x+3﹣h代入y=x2﹣4x+3,得x2﹣4x+3=﹣x+3﹣h.
整理得:x2﹣3x+h=0.
∵直线EF与抛物线没有交点,
∴△=(﹣3)2﹣4×1×h=9﹣4h<0,
解得h> ![]() .
.
∴当h> ![]() 时,直线EF与抛物线没有交点;
时,直线EF与抛物线没有交点;
(3)解:∵y=x2﹣4x+3=(x﹣2)2﹣1,
∴顶点C(2,﹣1).
设直线AC的解析式为y=mx+n.
则 ![]() ,解得
,解得 ![]() ,
,
∴直线AC的解析式为y=﹣2x+3.
如图,设直线AC交x轴于点D,则D( ![]() ,0),BD=
,0),BD= ![]() .
.
∴S△ABC=S△ABD+S△BCD= ![]() ×
× ![]() ×3+
×3+ ![]() ×
× ![]() ×1=3.
×1=3.
∵直线x=m与线段AB、AC分别交于M、N两点,则0≤m≤2,
∴M(m,﹣m+3),N(m,﹣2m+3),
∴MN=(﹣m+3)﹣(﹣2m+3)=m.
∵直线x=m把△ABC的面积分为1:2两部分,
∴分两种情况讨论:
①当 ![]() =
= ![]() 时,即
时,即 ![]() =
= ![]() ,解得 m=±
,解得 m=± ![]() ;
;
②当 ![]() =
= ![]() 时,即
时,即 ![]() =
= ![]() ,解得 m=±2
,解得 m=±2
∵0≤m≤2,
∴m= ![]() 或m=2.
或m=2.
∴当m= ![]() 或2时,直线x=m把△ABC的面积分为1:2两部分.
或2时,直线x=m把△ABC的面积分为1:2两部分.
【解析】解:(1)∵直线y=﹣x+3交坐标轴于A,B两点,
∴A(0,3),B(3,0),
把A(0,3),B(3,0)代入y=x2+bx+c,
得 ![]() ,解得
,解得 ![]() .
.
所以答案是﹣4,3;

 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案