题目内容
如图,双曲线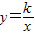 与直线y=mx相交于A、B两点,M为此双曲线在第一象限内的任一点(M在A点左侧),设直线AM、BM分别与y轴相交于P、Q两点,且
与直线y=mx相交于A、B两点,M为此双曲线在第一象限内的任一点(M在A点左侧),设直线AM、BM分别与y轴相交于P、Q两点,且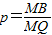 ,
,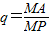 ,则p-q的值为 .
,则p-q的值为 .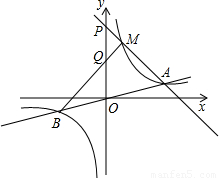
【答案】分析:设A(m,n)则B(-m,-n),过A作AN⊥y轴于N,过M作MH⊥y轴于H,过B作BG⊥y轴于G,根据平行线分线段成比例定理得出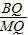 =
=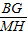 ,
,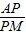 =
=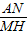 ,求出p=1+
,求出p=1+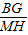 ,q=
,q=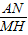 -1,代入p-q求出即可.
-1,代入p-q求出即可.
解答:解:∵双曲线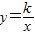 与直线y=mx相交于A、B两点,
与直线y=mx相交于A、B两点,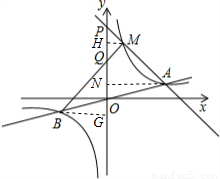
∴设A(m,n)则B(-m,-n),
过A作AN⊥y轴于N,过M作MH⊥y轴于H,过B作BG⊥y轴于G,
则BG=AN=m,
∴MH∥AN∥BG,
∴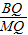 =
=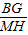 ,
,
∴p=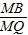 =
=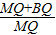 =1+
=1+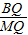 =1+
=1+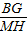 ,
,
∵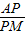 =
= ,
,
∴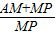 =
=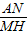 ,
,
即1+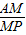 =
=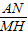 ,
,
∴q=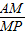 =
=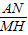 -1,
-1,
∵BG=AN,
∴p-q=(1+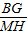 )-(
)-(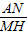 -1)=2.
-1)=2.
故答案为:2.
点评:本题考查了平行线分线段成比例定理和一次函数与反比例函数的应用,关键是根据平行线分线段成比例定理得出比例式,题目比较好,但有一定的难度.
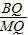 =
=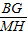 ,
,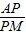 =
=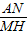 ,求出p=1+
,求出p=1+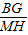 ,q=
,q=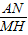 -1,代入p-q求出即可.
-1,代入p-q求出即可.解答:解:∵双曲线
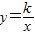 与直线y=mx相交于A、B两点,
与直线y=mx相交于A、B两点,
∴设A(m,n)则B(-m,-n),
过A作AN⊥y轴于N,过M作MH⊥y轴于H,过B作BG⊥y轴于G,
则BG=AN=m,
∴MH∥AN∥BG,
∴
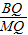 =
=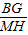 ,
,∴p=
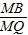 =
=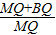 =1+
=1+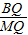 =1+
=1+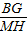 ,
,∵
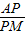 =
= ,
,∴
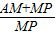 =
=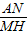 ,
,即1+
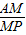 =
=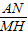 ,
,∴q=
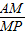 =
=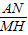 -1,
-1,∵BG=AN,
∴p-q=(1+
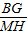 )-(
)-( -1)=2.
-1)=2.故答案为:2.
点评:本题考查了平行线分线段成比例定理和一次函数与反比例函数的应用,关键是根据平行线分线段成比例定理得出比例式,题目比较好,但有一定的难度.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
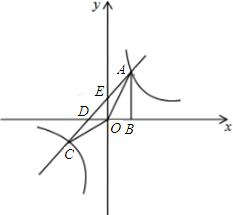 如图,双曲线
如图,双曲线 与直线y=x+(k-1)在第一象限的交点为A,在第三象限的交点为C,过A作AB⊥x轴于点B,且S△ABO=1.5.
与直线y=x+(k-1)在第一象限的交点为A,在第三象限的交点为C,过A作AB⊥x轴于点B,且S△ABO=1.5.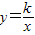 与直线x=k相交于点P,过点P作PA⊥y轴于A,y轴上的点A1、A2、A3…An的纵坐标是连续整数,分别过A1、A2…An作x轴的平行线于双曲线
与直线x=k相交于点P,过点P作PA⊥y轴于A,y轴上的点A1、A2、A3…An的纵坐标是连续整数,分别过A1、A2…An作x轴的平行线于双曲线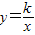 (x>0)及直线x=k分别交于点B1、B2,…Bn,C1、C2,…Cn.
(x>0)及直线x=k分别交于点B1、B2,…Bn,C1、C2,…Cn.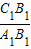 及
及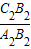 的值;
的值;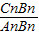 的值(直接写答案).
的值(直接写答案).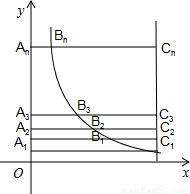
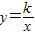 与直线x=k相交于点P,过点P作PA⊥y轴于A,y轴上的点A1、A2、A3…An的纵坐标是连续整数,分别过A1、A2…An作x轴的平行线于双曲线
与直线x=k相交于点P,过点P作PA⊥y轴于A,y轴上的点A1、A2、A3…An的纵坐标是连续整数,分别过A1、A2…An作x轴的平行线于双曲线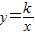 (x>0)及直线x=k分别交于点B1、B2,…Bn,C1、C2,…Cn.
(x>0)及直线x=k分别交于点B1、B2,…Bn,C1、C2,…Cn.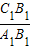 及
及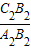 的值;
的值;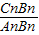 的值(直接写答案).
的值(直接写答案).
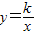 与直线y=ax+b相交于点A(1,5),B(m,-2).
与直线y=ax+b相交于点A(1,5),B(m,-2).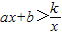 的解集(直接写出答案).
的解集(直接写出答案).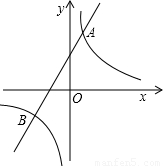
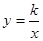 与直线x=k相交于点P,过点P作PA⊥y轴于A,y轴上的点A1、A2、A3……An的坐标是连续整数,分别过A1、A2……An作x轴的平行线于双曲线
与直线x=k相交于点P,过点P作PA⊥y轴于A,y轴上的点A1、A2、A3……An的坐标是连续整数,分别过A1、A2……An作x轴的平行线于双曲线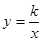 (x>0)及直线x=k分别交于点B1、B2,……Bn,C1、C2,……Cn.
(x>0)及直线x=k分别交于点B1、B2,……Bn,C1、C2,……Cn.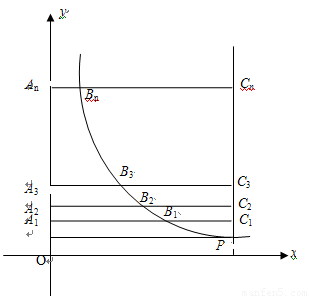
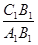 及
及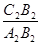 的值;
的值;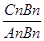 的值(直接写答案).
的值(直接写答案).