题目内容
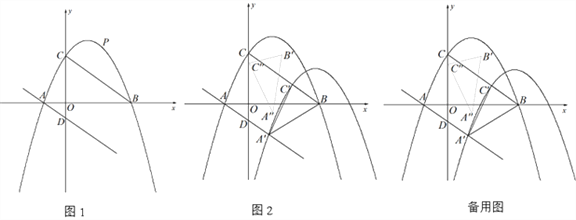
【题目】如图,在平面直角坐标系中,抛物线![]() 与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,连接BC,过点A作AD//BC交y轴于点D.
与x轴交于A,B两点(点A在点B左侧),与y轴交于点C,连接BC,过点A作AD//BC交y轴于点D.
(1)求平行线AD、BC之间的距离;
(2)如图1,点P为线段BC上方抛物线上的一动点,当△PCB的面积最大时,Q从点P出发,先沿适当的路径运动到直线BC上点M处,再沿垂直于直线BC的方向运动到直线AD上的点N处,最后沿适当的路径运动到点B处停止.当点Q的运动路径最短时,求点M的坐标及点Q经过的最短路径的长;
(3)如图2,将抛物线以每秒![]() 个单位长度的速度沿射线AD方向平移,抛物线上的点A、C平移后的对应点分别记作
个单位长度的速度沿射线AD方向平移,抛物线上的点A、C平移后的对应点分别记作![]() ,当
,当![]() 是以
是以![]() 为底边的等腰三角形时,将等腰
为底边的等腰三角形时,将等腰![]() 绕点D逆时针旋转一周,记旋转中的
绕点D逆时针旋转一周,记旋转中的![]() 为
为![]() ,若直线
,若直线![]() 与y轴交于点K,直线
与y轴交于点K,直线![]() 与直线AD交于点I,当
与直线AD交于点I,当![]() 是以KI为底边的等腰三角形时,求出
是以KI为底边的等腰三角形时,求出![]() 的值.
的值.
【答案】(1)平行线AD、BC之间的距离为![]() ;
;
(2)点M的坐标为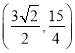 ,点Q经过的最短路径的长为
,点Q经过的最短路径的长为![]()
(3)![]() 的值为
的值为![]() .
.
【解析】试题分析:(1)(1)先求出抛物线与x轴和y轴的交点坐标,再用勾股定理求出BC 的长, ![]() 求得
求得![]() 的值,
的值, ![]() ,由
,由![]() 得出BH的长;(2)
得出BH的长;(2)
先判断出△PCD面积最大时,点P的坐标,然后判断出所走的路径最短,即最短路径的长为![]() 的长,计算即可;(3)
的长,计算即可;(3)![]() 是等腰三角形,分三种情况分别建立方程计算即可.
是等腰三角形,分三种情况分别建立方程计算即可.
试题解析:(1)令![]() ,
,
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
(2)![]()
![]()
![]()
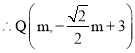
![]()
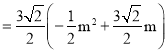
![]()
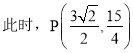

![]()
![]()
![]()
(3)![]()
![]()

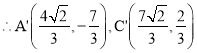
![]()
![]()
①,![]()
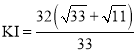
②,![]()
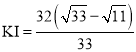
③,![]()
![]()

练习册系列答案
相关题目