题目内容
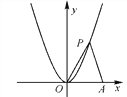
【题目】如图,点P是抛物线y=x2在第一象限内的一点,点A的坐标是(3,0).设点P的坐标为(x,y).
(1)求△OPA的面积S关于变量y的关系式;
(2)S是x的什么函数?
(3)当S=6时,求点P的坐标;
(4)在y=x2的图象上求一点P′,使△OP′A的两边OP′=P′A.
【答案】(1)S=![]() y(y>0);(2) S是x的二次函数;(3) (2,4);(4) (
y(y>0);(2) S是x的二次函数;(3) (2,4);(4) (![]() ,
, ![]() ).
).
【解析】试题分析:(1)△OPA的高为P点的纵坐标,底边为A的横坐标,所以得到关系式S=![]() y;(2)由S与y的关系得到S=
y;(2)由S与y的关系得到S=![]() ,所以S是 x的二次函数;(3)将S=6代入函数表达式S=
,所以S是 x的二次函数;(3)将S=6代入函数表达式S=![]() y,S=
y,S=![]() 就可得到P点的坐标;(4)OP′=P′A,则
就可得到P点的坐标;(4)OP′=P′A,则![]() 在OA的垂直平分线上,所以作OA的垂直平分线与抛物线y=x2的交点即为P点,求出P点的坐标。
在OA的垂直平分线上,所以作OA的垂直平分线与抛物线y=x2的交点即为P点,求出P点的坐标。
解:(1)S=![]() y(y>0).
y(y>0).
(2)S=![]() x2(x>0),S是x的二次函数.
x2(x>0),S是x的二次函数.
(3)∵S=![]() x2=6(x>0),
x2=6(x>0),
∴x=2.
∴y=x2=4.
∴点P的坐标为(2,4).
(4)∵OP′=P′A,∴P′在OA的垂直平分线上.
∴P′的横坐标为![]() .
.
当x=![]() 时,y=x2=
时,y=x2=![]() .
.
∴点P′的坐标为(![]() ,
, ![]() ).
).

 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案【题目】某社区超市第一次用6000元购进甲、乙两种商品,其中乙商品的件数比甲商品件数的![]() 倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
倍多15件,甲、乙两种商品的进价和售价如下表:(注:获利=售价﹣进价)
甲 | 乙 | |
进价(元/件) | 22 | 30 |
售价(元/件) | 29 | 40 |
(1)该超市购进甲、乙两种商品各多少件?
(2)该超市将第一次购进的甲、乙两种商品全部卖完后一共可获得多少利润?
(3)该超市第二次以第一次的进价又购进甲、乙两种商品,其中甲商品的件数不变,乙商品的件数是第一次的3倍;甲商品按原价销售,乙商品打折销售,第二次两种商品都销售完以后获得的总利润比第一次获得的总利润多180元,求第二次乙商品是按原价打几折销售?