题目内容
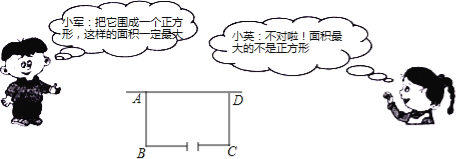
【题目】如图,△ABC中,∠ACB=90°,将△ABC沿着一条直线折叠后,使点A与点C重合(如图②)
(1)在图①中画出折痕所在的直线l,问直线l是线段AC的 线;
(2)设直线l与AB、AC分别相交于点M、N,连结CM,若△CMB的周长是21cm,AB=14cm,求BC的长.

【答案】(1)垂直平分;(2)7cm
【解析】
(1)由折叠的性质可得AN=NC,∠ANM=∠CNM=90°,即直线l是线段AC的中垂线;
(2)由折叠的性质可得AM=CM,即可求BC的长.
(1)如图①,

∵将△ABC沿着一条直线折叠后,使点A与点C重合,
∴AN=NC,∠ANM=∠CNM=90°,
∴直线l是线段AC的垂直平分线,
故答案为:垂直平分;
(2)∵将△ABC沿着一条直线折叠后,使点A与点C重合,
∴AM=CM,
∵△CMB的周长是21cm,AB=14cm,
∴21=CM+BM+BC=AM+BM+CB=AB+BC=14+BC,
∴BC=7cm.

 名校课堂系列答案
名校课堂系列答案【题目】数学课上,李老师出示了如下框中的题目.
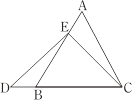
在等边三角形ABC中,点E在AB上,点D在CB的延长线上,且ED=EC,如图.试确定线段AE与DB的大小关系,并说明理由. |
|
小敏与同桌小聪讨论后,进行了如下解答:
(1)特殊情况,探索结论
当点E为AB的中点时,如图1,确定线段AE与的DB大小关系.请你直接写出结论:
AE DB(填“>”,“<”或“=”).

图1 图2
(2)特例启发,解答题目
解:题目中,AE与DB的大小关系是:AE DB(填“>”,“<”或“=”).
理由如下:如图2,过点E作EF∥BC,交AC于点F.
(请你完成以下解答过程)
(3)拓展结论,设计新题
在等边三角形ABC中,点E在直线AB上,点D在直线BC上,且ED=EC.若△ABC的边长为1,AE=2,求CD的长(请你直接写出结果).