题目内容
【题目】(1)某城市自今年6月调整出租车价格,新标准规定:出租车起步允许行驶的最远路程为3千米,超过3千米的部分按每千米另收费.甲说:“我乘这种出租车走了8千米,付了24.5元;”乙说:“我乘这种出租车走了13千米,付了36元”.请你算一算这种出租车的起步价是多少元?以及超过3千米后,每千米的车费是多少元?
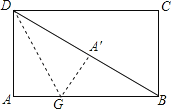
(2)如图,长方形纸片ABCD中,AB=4,AD=3,折叠纸片使AD边与对角线BD重合,折痕为DG,求AG的长.
【答案】(1)这种设这种出租车的起步价为13元,超过3千米后的每千米收费2.3元;(2)AG=![]() .
.
【解析】
试题分析:(1)设这种出租车的起步价为x元,超过3千米后的每千米收费y元,根据题意列出两个二元一次方程,解方程求出x和y的值即可;
(2)根据勾股定理可得BD=5,由折叠的性质可得△ADG≌△A′DG,则A′D=AD=3,A′G=AG,则A′B=5﹣3=2,在Rt△A′BG中根据勾股定理求AG的即可.
解:(1)设这种出租车的起步价为x元,超过3千米后的每千米收费y元.
![]() ,
,
解得![]() .
.
所以这种设这种出租车的起步价为13元,超过3千米后的每千米收费2.3元;
(2)解:在Rt△ABD中,BD=![]() =
=![]() =5,
=5,
由折叠的性质可得,△ADG≌△A′DG,
∴A′B=AD=3,A′G=AG,
∴A′B=BD﹣A′D=5﹣3=2,
设AG=x,则A′G=AG=x,BG=4﹣x,
在Rt△A′BG中,x2+22=(4﹣x)2,
解得x=![]() ,
,
即AG=![]() .
.

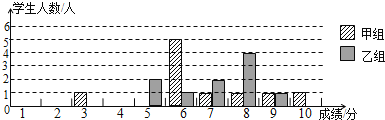
【题目】某校团委举办了一次“中国梦,我的梦”演讲比赛,满分10分,学生得分均为整数,成绩达6分以上为合格,达到9分以上(含9分)为优秀.这次竞赛中甲、乙两组学生成绩分布的条形统计图如下.
(1)补充完成下列的成绩统计分析表:
组别 | 平均分 | 中位数 | 方差 | 合格率 | 优秀率 |
甲 | 6.7 |
| 3.41 | 90% | 20% |
乙 |
| 7.5 |
| 80% | 10% |
(2)小明同学说:“这次竞赛我得了7分,在我们小组中排名属中游略偏上!”观察上表可知,小明是 组学生;(填“甲”或“乙”)
(3)甲组同学说他们组的合格率、优秀率均高于乙组,所以他们组的成绩好于乙组.但乙组同学不同意甲组同学的说法,认为他们组的成绩要好于甲组.请你给出两条支持乙组同学观点的理由.